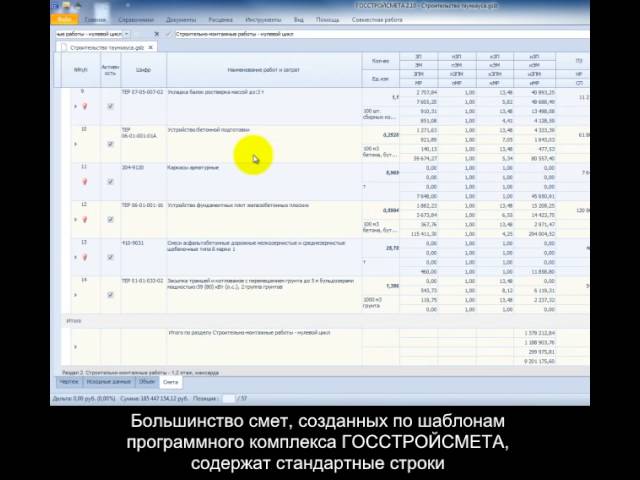
Применяется ли коэффициент К=1,1 по Прил.9.3 п.2 монтаж конструктивных элементов по железобетонным и каменным опорам к расценкам таблицы ФЕР09-01-03?
Коэф. по Прил.9.3 п.2 Монтаж по ж/б и каменным опорам
05.05.2025 09:44:16 | |
Похожие темы:Найти еще: монтаж
Расценки по Реле
Автор: Карина. Доброе утро дорогие специалисты! Может у кого есть смета, впервые столкнулась с реле, помогите пожалуйста...В ведомости: 1. Монтаж реле АПВ 2. Монтаж указательных реле 3. Монтаж промежуточных реле 4. Монтаж реле времени (вроде как нашла расценку м10-01-039-06, если правильно....
Автор: Карина. Доброе утро дорогие специалисты! Может у кого есть смета, впервые столкнулась с реле, помогите пожалуйста...В ведомости: 1. Монтаж реле АПВ 2. Монтаж указательных реле 3. Монтаж промежуточных реле 4. Монтаж реле времени (вроде как нашла расценку м10-01-039-06, если правильно....
Прошу скинуть смету на монтаж грузового мачтового подъёмника
Автор: Ирина. Прошу скинуть смету на монтаж грузового мачтового подъёмника: (монтаж основания подъёмника, подключение к эл. сети, пусконаладка, монтаж второй секции, рядовой ...
Автор: Ирина. Прошу скинуть смету на монтаж грузового мачтового подъёмника: (монтаж основания подъёмника, подключение к эл. сети, пусконаладка, монтаж второй секции, рядовой ...
Расценки на монтаж футбольных ворот, монтаж скамеек с навесом и монтаж поручней
Автор: Ирина. Работаю в базе ТСН. Помогите найти расценки на монтаж футбольных ворот, монтаж скамеек с навесом и монтаж поручней из нержавейки. Может у кого есть готовая смета в этой базе? Заранее благодарю!...
Автор: Ирина. Работаю в базе ТСН. Помогите найти расценки на монтаж футбольных ворот, монтаж скамеек с навесом и монтаж поручней из нержавейки. Может у кого есть готовая смета в этой базе? Заранее благодарю!...
Система "Струна". Правильность применения расценок
Автор: Елена. Доброе всем утро!!! Подскажите пожалуйста, правильно ли я подбираю расценки на следующие виды работ: 1. Монтаж системы "Струна" (ТЕРм11-02-032-01) 2. Монтаж вентиля запорного фланцевого (ТЕРм12-14-020-03) 3. Монтаж предохранителя огневого (ТЕР09-02-015-03) ...
Автор: Елена. Доброе всем утро!!! Подскажите пожалуйста, правильно ли я подбираю расценки на следующие виды работ: 1. Монтаж системы "Струна" (ТЕРм11-02-032-01) 2. Монтаж вентиля запорного фланцевого (ТЕРм12-14-020-03) 3. Монтаж предохранителя огневого (ТЕР09-02-015-03) ...
Как осметить датчики температуры
Автор: Елена. Добрый день Всем!!! Подскажите пожалуйста, как осметить следующие позиции: 1.Монтаж датчика PWD12 2.Монтаж базовго блока RWS200 3.Монтаж барометра PTB 110 4.Монтаж бесконтактный датчик температуры поверхности дороги ...
Автор: Елена. Добрый день Всем!!! Подскажите пожалуйста, как осметить следующие позиции: 1.Монтаж датчика PWD12 2.Монтаж базовго блока RWS200 3.Монтаж барометра PTB 110 4.Монтаж бесконтактный датчик температуры поверхности дороги ...
05.05.2025 13:35:43
"Выберите себе работу по душе, и вам не придётся работать ни одного дня в своей жизни." © Конфуций | |||
05.05.2025 14:09:59
я так и думала, что все позиции перечня коэффициентов, который открывается в доп. информации о позиции можно применять для данной позиции, но
| |||
05.05.2025 14:24:45 | |
05.05.2025 14:31:59
Я совсем запуталась. Получается, чисто технически в программе, не вникая в то, опоры там или ж/б фундамент и т.д., я могу применить этот коэффициент?
| |
05.05.2025 14:37:49 Elena, с чем вы запутаться-то умудрились? Прил.9.3 п.2 - применяется для всех расценок ФЕР09, если есть условия под этот пункт. В целом К, Монтаж конструктивных элементов по железобетонным и каменным опорам, применяется когда вы любую МК крепите к к жб или бетонному основанию. Иными словами этот коэф учитывает к примеру - сверление отверстий в бетоне и установку анкеров. Есть у вас это в ПД - применяйте, нет - не применяйте. | |
05.05.2025 16:31:22
| ||||