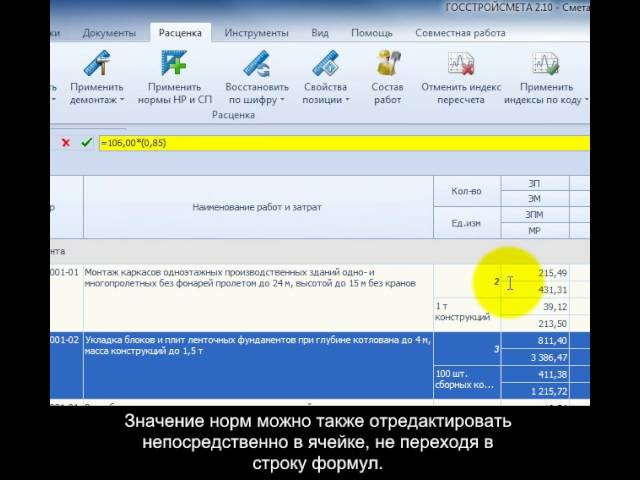
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAtoAAABOCAYAAAAehrFPAAAgAElEQVR4Ae1dCZbrOAjsc+VAPk9Ok8vMYTIPSQWFFrx08nvjvzdjWwsUBUiynLY/nvkvGUgGkoFkIBlIBpKBZCAZSAZezsDHyyWmwGQgGUgGkoFkIBlIBpKBZCAZeOZCO4MgGUgGkoFkIBlIBpKBZCAZeAMDudB+A6kpMhlIBpKBZCAZSAaSgWQgGciF9jti4L/787Y93iH5e8v8q3Z/b68kumQgGUgGvoyB/+63J6bD++32vP/3ZVBScTLwJQy8YaH9eG4fH8+P8t+5pLrf0G97Hl+mQt+ZPle5hi7B6W17bMBejxhYrmr6Kf3+qt0/xT+JMxlIBpKBL2VANmCwJvgrE+OXEp7KvxsDL19oy2JZc+mxPT9u90M2y13vDbe60k+FxN2h735790K7LrIVlmD8aDplIDloZ2zND6v9q3b/MDcl3GQgGUgGkoFkIBn4GgZevtD2Zjye28EF6GPzO8RnF85n23ucB64em90ItOb6SEzqts3u2j/sZsPv+HobRYzIqLv/fpe87u779rbj79uaDN/+gFWlSZF7uz8Zq95Q9BjZn4HdRTDvZPATAFeOJwHXsBc95aYHcuyoNjh9n9DzfD7XfmlyV7qAsYEC1+XS9QF+w2n+/XA3rgXL9jC/3e4V3+2mT5WUA+hnPxwNEG3nn+hs21YfAwf492Lr6fqazZXnD7vhBn4xyPXZ4auzF7xbzjUdKtMwmNlyU21YIGN7gA/rY766Pe/31q/ckKOtjQ0q/+DJXuyZbuHEMJ3ii/P7+bTYwo7khIeey6XvIKPoMD6wwbLEX/ix9mKbxh7iotlrvkGumt+eaCsxhPMX+cbkVd4ZR4Gv8dX5Bjhaog79ngu7nTyfA+ucM1nTcUHjdbRBfdM6ciwu/b092ni58MHBuJ82c/ZTrINPxFo7Cuw1L1WD2lj6kMydPLja7+l8W30ouQA+b/e7juNuU6+zzeW6k0l5Ukw0/yNnkXtTjncLWV6va7czNTA5s7i84ZcOZ8cNFyM+R4pyV2/+5tgGyFkZ6o4c37rQlgBU4nbQSFt1ekkWM3yna6l+90J7aktbfNdEY7wSOPUaNxDT/uJontj4upzf7Lfeout2KwuPmSzoOcLV2KYFujrL8Je2j4f+lEd0w0+R3XUQIU5KUNMTgKYLfvscfpk3O10rWxjHSMR+SeCX0OYyWC8wisyIjwX/wt0mP1kqE5rEx8ezDM4SUyQTRjmOUHjiKION0lp4bPaQrtGfUWx1cVZk4skU36Q3GciVSJ/UoZ3Y1l+Xm6WZji6GOl4cd6R/LxdLjjQ8sohS/jr5hy6LLfMxYbCT7Sa8o38kMOf5DUzoU+KbuV1yufadyWq+ASGMVxR318vYaxsBRYzMG9ujbF5UsWscVcVNb1w/7Zs9HMOND2KwizvylWBc2k3twKnFaJBz1A/+tX5Ce5uzBy4Fi2GWGwvMAz4uulyVhZ/GTF8HBGePIqcbS/F0ORpnsQhFzJVrGsMU5xh/1Rewn2zq4rSP22U/qWAO2S/tvNx0AWvzR5HfyuAP9t8yXiJ9UnfhX6jrrDy2v/X1doH75hvwEvFPMkeughgqMhfj7Fm7Wvu3LbR5gjmGrSVhu5uURSV+SXKkP4g80vZKGx2AuDMttG3QaQ1aHYKl8EF3ohInfVm9y6TEb7uVdedsez5o8MMdqRxFFvQwvOPnwj0FsnSkQaDHCVulHOeqC/1w1AoaxMMEoA4nTp39JJ/tgDjBjTxF2eFjk10n5sYbBsHI5kIp7qrbESAIL+KY7VnxD8wy4JV44Imi6YMKHqDR79SRMA79qG7EH8RWyJdNZso17Av09Vy5nGrAgdEvECTkvX+Uu8B3vT7pw74TldqGBQ4kHihodisfkrOLMcHZHfDl8LXxqc/pFV/Sd1639p21bzuMjRPliMZI3akj/DOWrG83htEiTzlDDDVB2vezvmE/B2Mp8IteqOzjTn82GdlNdeDU4i7IuZ1xQfnobXC+LkJo7F/7m3Ns5QNwcvgYjhtd/hFPBUtvV5NldvMY4Ncg4Jltutqv2Ip5Qy4Yp5y3dZCtgRrH1A541O9UN+VypW/aeKdwT9dO91l1jY9W08mHrVJb5ruT4wb6K1dRDDXdGq80zs5wHyl7y0K7DBzdgHYEDLcBMVwWnZ9tH8ma1kWOeWw6aGrfrj0PrHrX27XRvnKigSaDZtsJo0kVgzRkaQA5IUcvbKDUHsAmOHhwQrk0jOzmdk2o46CVvcpvzn7lrp8QqtIZjgZn/6CyR7/sLeqXGEnrwEfEf5vcZWEk/e7DjY/51ekmfYdP1e64x4CfFjvaE7GBo1bQzRj66eRgtlBzWui10olMbi/nhtHLdByJvTSGDXU00O/looyHeBrVYzl1rT44Fnsz2WZ7q92JL2llfTxf67rWbuK7MjdgQS8/twN5kd/U7plFFDOij3ymC6IJDkh6mW9aLhZzehwT23gMWsWWzQFAOz+af1A/+smPTVbvdEc2uDjox9W1v4/4AKgPH6/yiTGFFUEWjlzXnRvPxp/ntevQLqf9tI4W9siFFu/eN6RT+3Y3ljt5It10U0ZyEPqavFOHA7pOySuNzUZvu98EKT/TBfYDfhPR5oOGatJPc1Jtm4yz540qPV6+0Oa7jRkmMQa7sLN6KZM2/a7KXr+ByCZ8r98Kw1hOpEulDKa6AH08Nzi+dewDRXBoE+fILlmgWNugoOl0j0YLWWWy6vVRrwOn1TbmXOV1OMS/1i6y25IGAGY+mpWh/Zmj4pVODvMxHId1OdmtVzCRs31rjKad25fSTp/n3wYQ9MMREkvc3e2nKSi/cuxfzVUWKbblUkT2+usuEscM7zhFvpE6+a058mNsKwrn+tDHW1nbSqyj3ssc/EOLtqGuJfMsr7ltWVi2tnzukR286mKh9OLYU7vW8ga+OpkcXxFfUV1dXO37bsjTAH8Ue+wD4VjH2bKwWuNgf/D5mr24JsbhXwrAfuB48ZxIfPtdVcFp42/Fw7JqSTCeNxNW48Lahi7X3EIlytWoLuZzXevzVtoxB2s+I154XJho1jyTOta/7hfnSLeG4Dxs5+ILLIb5HOjYZisL4oXXLKwPnU8ej8TmSZH1p0t785XDvuafdY9csQ9rS23j5Dcpzv8s+dj5axfaAtA9+pO7NUxqFVAJGOzQEkaUzx6BSzPU2yBaO5eFvdN5TB+pPnFaE9U9lm29y0DNOBjohBetLsFPd7WFL9LTJnvYX3Vz+7ZbVnT7JDtuWA06x6UC7O4m5Xfi5L/I7h4zTxBR3XHctaXJEt8bd9Bn9ZU3lJ/Vg0UjxyjLFsr4WtpBl5Wfx8gcl53Rwn+1U+Rr/e3e9HMcSDu+Pm+19ujjmGLE7Os5jmNr1Q+xCBW4dhMP5Rt4LlinOSWTccVWZVqcFJm9bRTjhrH3Hf+xUrO75Uf9gz38oXPf78qLhAnvZEwoNi3sFk7Mht4/6/yO+DpeZ7zDd4IH/TlH6uZFxVdyjOeO3j8IDLW5xTja4Q+DyY+qs21WmA7j1sWRBv6BkwBHxL/5ZREjsAexDrtDn8Y5V62ZjAuBDTrGAAeO9AePgMY843xWd4DVZRPjzcezlc/43OFF7UcMiowxd2rc0I7wop+33WKMx5vKi9XxH0BKLEIGr6PMRm97IWsVL6181HdlLGpuWelaeu1IxSQuqZvxYXNrNG5EXM3rzBd4OsbtEMcE6dDpaxfah1Rmo+/HQB2Avh+uRHSZARkEZVRwO0+XpX2iY8bWJ8jLrsnABQaCnHvluABZFxB+TZeAlwCQLLSGBdaPsz0w8DtUgc8vn6/eQ0YutN/D64+SyneJw4DyoyxJsMqADFxl16nuymj5Pz7J2PrHhKe6P89AmHPfZFz4CieFvHwFoNRpDPzyuMyFtrk6z5KBZCAZSAaSgWQgGUgGkoGXMZAL7ZdRmYKSgWQgGUgGkoFkIBlIBpIBYyAX2sZFniUDyUAykAwkA8lAMpAMJAMvYyAX2i+jMgUlA8lAMpAMJAPJQDKQDCQDxkAutI2L33uGv+j9hhbyX3T37+X8hnATUjLwoxjI/PpR7kqwyUAy8AsZyIX2L3SqmNS/9/Tbvk1E/9qY3kv6S32SZiUD/5yBzK9/TnkqTAaSgWSAGciFNrPxW85lcqWv2v0Ws9KOZCAZSAaSgWQgGUgGfhIDb1ho05d1Pm7Pbdue+Epzv8tavrDUtlr56zvyVTX0ETLn/bbn1r5Opbu1+oUmfJFNvh7EX2+r7xSu79MUbLXdbdvqO4fpa2L6FTPIFCU4777eqPqveJ53nPC1rWZ/wXm7O/tZ15Izeek7bOo5EoxOJ3Gt9uHLWPT1pf4LWbyQR78GDv6SS313KYBT26gOVMJGdEf5lSP8zrHFZdBV4pLtK8rWce2+GNnFfCzzihULHM6n8J/5NsIBf+kXzyRmhHCVaXIUMflRyiBjewCf9THdt+f9vpUvi9YvnaEtfzZbNRw/AZaWN4aliVA7hBfDpfncgmvoR18ZrV96bGOZk+e5LvE0zdmJrYxbean4GIvy13ByzNZzehoEmfTFvulYdpzdwy3XWGysRozpFxiBV8e+zkeOa/KdK/c+EMDKmcjlXJ7oUywUx8BZjntc7shcYulxUmyyj+EA5bdwZVyY/HfnF3iuRx2TnS8MF3CfOaqNEA5u5ZrPyVfW1OP7rO9CLKTfx4rFOnAp7uZf81cXm0uZ7xmLK27vr1ncnfGf2ep9IVwU2dOxsWkI4shxRnli+qodPG7a/MVYzF4nk8aIGQezsjO8vHyhLYA0wApxZpgA0+/JyyQG46QdzqVRfx31U2XV7MfW9ImM7VEXAGgjiSrnrY7xaD/GhYmWsBXntGtxKkRX7Rf+v4cFi54iWiZrso9wMWc1gJh36ldsojrRT586lr5mE/lI9D/kA+f1n7TzE1QnU4WwjLbYUNxRnemRAUHFNf2XDmLr7Va/mCgC5IZEPpkN4YF9UVxHdRFnV2xY6grjKPad4JjmZaGI/NoBtpxpOdt49DFUO3HbEp+vzKG2YCnqW44bBo79hpPinXHxuFA5obgredK4CLluMY6Y4nyjfqCS9SvmwQb2T4tbvVuMciiqA4JXHo/rs3ir+vnaOAl8R1yir/WL4115LqoZc4+F67rzbgEfylyNK2KDjoXdvFfq5mOV11Uxs+1Sj5uLl8xR/ThA3NdNBhojpI7yq6I78/+YZ7azz1fRglgouJTbWKbns2vLMjqfL/U5fqrtDvcqHhpNcxtkuiKeW1scXB3p97Z1WKRdNB9C+MnjCotuSM3GRh4nRR/HUcF5NxTdtdrYj5vSrukCpw7byg9F/jz3DMS5s9cutMmwFQwYzIlQBoZylz6/8xBZs35S7gYS1i/nRSYHZ0siage55gBLtCrbrmGT4tWAQc2F4x6WftBqnyhVDI63aqvU8SK4oMKnTXEkqNIepvRyUS7N+zrWIVz5O3ssyY2/kc+ojgC+6rRxrTiEW9x8RfaRjwYoUV0kcxB0oCDSRXVjTMe+E83ow3kp5b1fOR76Otyw9HEifSy/qp3ahgUeoGDVROUt8oX7SVuoXdkwm8RVRsi1LA67r3FSztXYa5JIjpQsbXD+KU6h/I5yKKpTa154EuuTm0SMETx2CACLP4oV4g0g1XfEHfpyjBmXVSfr6+sQC9ABeT4XYtsimX0dsPTlboex2VfjpcUULSTAoxz/RX4xty43Ih+B0FPHmOdlvjYdr/VdjEVUzvUF6xKX52Ns7sns/Q5qV7z0MeZiJYgxyL1yXMZKWUwvxsYgjnobXJ44PjvZV8eIN/DyLRbaZWdRd2jmrl0FNA+GMwe7MnG03KGGDmhtdAFmyQZkEtRuJxQVnzyajRA06lauJoGJXtKmnzyifhLIaM/nhVveQecFRKff8Uz8qn+mfO5zrTa94kRx1V3HYjNwSd3KPu03AbFXt5I5EbVbFOmizkMcRba1ftbHx9zgV93hoQWRyCBsLoakvDwu5BveOhG9ModUp/iTMGrcEz/aNtqpI3uo63BqvKHK81dKXa5YveO2TRgak2yDm9AXC23EMca4qriOd9M64H3l8Xg+928YYh6VF8dbxcm+A3LuW8p24t3L6HbNHdfmq3gcqzdJGEMPj5sT+2CT5dM4Vjn8/yi/1CcCkHNjYoPDpwYdPYljaImjibdYeIHvkEtB/sz1CRjTP2DemRNWMgc5NEYMdS0YnS/6WFE/jjF21FuzdisszIn2Q/zgqBWUU5M6alY2KFbjJtoZp61EbF/54Q28vHahXQapyYR6/6/d+YlDcddhgVgHJpSDGjpqoEsZ96ttSjDd7TFBKW1kSZ3baROPKJF2R2rBIfJvC5x1gQB55S7SRlcCfO10CAax9cP/TtrhVC57fY/n1uFy/ShBpSfrdYlZxlT6XSrJlN0p7MyIDJPfDcTFXys+Y65FbvHfK386QjYU1hBbFBOVE29fvzAoN1vt5nBZtyOz6D/5v6UuksP+LMUBjtp2lZcTv1LsrHzuYqjp5racN3xOJpw+ZZ0i09w8jhfMD+PicUEAXOI6zNlqVsHaj1ct1oHb2+Bz1N88RDkU1VUshf/lOHLWDfv6INHx3o1BaDMb69l3aDeUBfEufThW6nUd4+JciG1byRxjiscVzjtY046dDaW0jVVO1z/KL+cvh014ocf6S1929i0vY57XOOoNKOZmHzuxTMdniQ/8XVncT/Jwrq8aV+T2ee64k7y2eIjj7w1jcYeFY2zpngMVax/trGeWcRTkSZfP/bgJuKfGiDfw8vKFdhlY+OcMbebAY8N6WQkvjwBsZtHHivXRQF14S7Dy4xI9R78aHfbbZb22xzLQXf8Aqwa3ymGsH6YL4rXv9tBFX/+HXLzghGPPHHsbTV4dxBSDYAUwUSCJ7vDbzUqdQO1RLfdb6hvk+T/WYJllN7ItgE2e6Dffih3ADti4Fjw4n9WBP8hGG5SfPxou7HhCtnAo8lf2FV2SfMw1AwrqQpnnjag3iQscbI/YZHG0ts37gDgS+3q76IbHdPU+5z8+bjkov4MvmO0PkF+aQxq37SYfuNvAbVhtTBDqrby34b/qGcgB3+Rz6+tlYoIHr8Vu6lcFC89+Q8JyebSBY6jy2PJ6J4eAAepxbWNB8zcaXIlH6gP5EIfrD/kdKDjEEY3Udz2PcAFiZ6xf+2Ad78Zz41DwtDgB3grN54KvozlEGnc2FB/RooH9x+NmsXDo62MR2HpbOQ4gs/7BLvjycngsIJcdOjXdc5lWP/rokAJqFPFsekYcVkd+Fd/u5Ejku2NYRn1mziTPy7RtfeA7CSOvz8ff68diwzCLMaSn2XLszPww+mhvbLS+FZuL2Wme8BpoHDcFcSRznpfE+2T+uMrL6xfax/xxuJUQNRgnE6AU4rjzaOGoMncndrTTW9vVhfZbVaTwZCAZeCEDQc6+cryCrM8gFxn9gv8z8rJvMvBFDITrhDdgCvUhN1+0LnkD/C8SGYyNX4ToX6n99gvtkIgyUcjdj9w9/b5/uMOV3YvhZuP3mZsWJQM/noEwZ7/beCW7RDmw/PiYSwO+GQPfLc+/CT3h2PhNML4Lxs9eaL+LlZSbDCQDyUAykAwkA8lAMpAMfJKBXGh/ksDsngwkA8lAMpAMJAPJQDKQDMwYyIX2jJUsSwaSgWQgGUgGkoFkIBlIBj7JQC60P0lgdk8GkoFkIBlIBpKBZCAZSAZmDORCe8ZKliUDyUAykAwkA8lAMpAM/DkG+K0y/fcUrpDx1oW2gHXvQryC8Lf00fdAtvc94nrbykdp8C5LmFv+QhfvYs3XBIGWPCYDyUAykAwkA8lAMvA+BvTNMd23Sy5qfONCW178/Ttfu3eRa/dFsvKlInGmvF5LFtLyNUq8o7C/Lh+BSS6v8p79koFkIBlIBpKBZCAZ+AoG3rfQ7t7Rql/hKbu09vUd7HjL7rd97cq+moadXe3P75Tmuw58cYw+wBDK3B72JcDbvX6VafIlIN5pru+BNGzisFnZypH6OOK/+3Nrn+8ubWVhvcl/daUtjyq2jRbe7WtS4GolfyjHrrly478WOLSngpD3/otL2HnX/ubf+rWy+klb9eHJGJh9FUvkgkLnZ8ai9vuvVOkNjeJdnLj4Mn3Tr4m1uDzFG9kgCJQf8hfec+xsfEU/cNPIgG65rDFNd/Jd2/KFL8bYfYVywWYsFzrKzbnFz2Ff0RdJOeb2YsfXm48jDmqdtRV7XdkqbgoxZttRnBGWFddarrzSl+AOxGqoEzLPxE6JlzVnLr45h/uxhmPf8Qz7WMeC68EPky/RKYGTE9jf5YDGqsPFeCayqMjFUCvnsogjn5Myf+Az4iJozYOTydwSrtkp40I9ly3lOm5Gn7l+XRxgjLJ1go1RUd0qxz8zju/LrH4HLsTG0r5P8AL+Tx+DOC6+vN3dnAQbqp+Ne+VRGkxk8rrF2d/FG7ia+XfZD/oaOMgol1GdkOU4tzwN7TtNcu3wtoW2GMwEizr3vXkxEp6Tc04qd90GCbQtg0YjhWRAtn7d0clopDYd0nbbaqDI+e0mWO/PDRge8iHx+k8crHYUmTfD3XaesRhqXZYHCxZzamkscsrnyrfno9kkbdVkaSRB4wqWalyFl3Pmy0wB7wXPgqO26FCoYg8lFPxUQDZb9Rz8S0Hh+l6qynkTiP7qZ2mx8hcm6SZXYlJxVcnB/8V+8lOxw54qOP1sByY1VURy2CbR3F+7HCFf9e3664v9QhvUFy0O9LrGossJtTWgs1SRTeCJ5Jb8uOSrutBVGMIPfCfnrWKMHfIN/KFP4QKshf/VOBDJ/ARO5Wnijx3aQz/LYlGJY+yB/SUEutxgGTOsIWdBDpd+bRyAjyA/9G3AtchpY26hjuTsUKnVMacdNxpT2n1+cpWj3TGXxj3RwbkBLgVR0U9cz1HW0ghrL4ev5XyZj0EcNCzIYXzOmyHO6zimm43kj9iPQW6AQwEgNpFMnXPbnK3X0nY1V32SF+bhzPll+zVuxvHI2SvjPNpyHIA31DXQUx/u9FvbIGne5SKPU0sfEubJPHWGX7R920Jb7grUpoHEOghigC8TbLc7YDuW4khb4BRRGCSD4IxlVkB659I5u+/bLyrqgq3hOrEA1gDsAwf2tDsw4U3bwlNS1+FEVXTsbel9su4b8F7GFn4CQTdV5JOZbEukEzFAMtGfE6i3Uf3VAGj9ceP9RExyIIL1841A3T2ax6vicLFOA8Fiwfyufrj71x0EGEeDo8Y6xx7HPPlm5m9fZgPYVC7HlWLxEqZXEQaqG2IHeUdCheuqOsDaZKoNMj6Bk0gmYSGV9ZTqBpx7/hiE+YIrscoLGbWTYkDKNG76xXpr5/pFnLHfW24gh8PYjzijOs9Gu4K/5HKv7UTAktPI/xM5rugiRyH+wLaQWwdschFgDeUSnjHO67zHcYU4AAL04fgM63b8sfRjWWDNx3F3k9aU27jBNnT9gzhnH8JGxtZz2vMCDs4eWQdjiOYx5t7lOHHBPsRQ3ttQ23x+/luPRTKNL8apMC6Csf8swa39P11os9H8U4lZ4Jo9ZrSWTUhCcEZttK4FvASr9Lv3u9a8sGddOkjUu7gSQDxgs4LJeZ+MCEC2//Goe+nctogSPTTRTcRPi7wcwe0De9qpKrQ7UTQCF8LDLkfo5I/XYsBkDH6OsLRuolN+A48bO5MWnMFWasJchgNU7yfIwpFk9qdmH8X9m/rt2qCxTVgaYL1JdYus3pr+uskJ5F7yleZlr89fG7etfMKr+TjAqvom40AkU/t5XP3VgBML7YC3XgZf7/rZN25P8AL7y4YwjSPOrkU/bTPhTOpW48mET4aL84Ez1YcW4/FaDFc5S04neC2mRgyuRDGf5Ej7OWn1IqqbYJ1ImBep3AnWg3KnPlvFQUNhfVqcEbpp3QQL+2PpR+Qcydd5ekemyu/nbOFsxz5RZ3Y05Qf7MdSj55fsBzeL8UjtLyAkPtpYMeGtx2m2k393+q1tCHa0JzIN92IM68GeuH7bQrtMmPgR7QyQJqpUijPGu7/arSYy38E5YptscxCURTItmNEPR39XV3ddVbfD3PRosEHv+miO7HZRQqef18MInM6iln+7xy3784D3jgeZsJSjMlDQJFwmZV+vmpyc2F/oo35CgZPR+avpxgK7LPL17gYCVkdK9NaEdbsYdBgC3sI4L2DpZoD1r7mpmLj+WD8xKbRB/k5Ac5JlNpyoc7avuES5yFnLZf/wOXpHx/4VTLPxh/1XZXV2uUkuwDqzWceBSKbE535uzHGueYt4kbrQz93v661tYP+ezJmPI866Oj+ecGyvLR052+Fa/HUphlvkRI+kuxvtGbapJR0PpQ3iqqvzHMW2rmPuGLense6Nc03gwEtgY23LeC3PojrefYUdrNfivZuTiw1+3rK2pnsmk+dcGYd0ygnsgxw5Mr5SfqBfGS8Rzyxs59xsOmv/ejxi+0X9f3esOdh/E2CI9VLFHMf91jbsjH3LPI3Hvgny3aK3LbTl7g8LnB4F7yToAq0MfLzNj4V3JZz7sFxxKj+mUHmidCpTnFYTqAbnR9kprnLqJKjl0k52QssfD9V+RVdzEOvWZOqNxbVisYmW9RS5TYiV+7a7OqALR9VJvHbBhabjMebdMDJHTYoMDPzziAlw9qf6bMCLGODHcdUW7VPcbPaZv7iPyDH/cd/Rbith/4p/0M/KZ3Jj3uYxyVjNFo6JVT/wWCk2GzVHFpxGNniZMvA3TKKk+bbXB26MvfEMchAOuBasEZ5R0qQkiDmTPcbOqg7YRqztdZwS34txYCWzoL6Ac40Ff0ky4aMVGZZzsRrpjGQu+2E8WHAWjieLGBYTDcvoW8RqySN+8vKJGPY6Z5zuYFq6inL3CkdBXC15ECwBt0uoNJauciCSG/lsFQc+roir7aHjUz8mYQxc6bPymR/jcdz6dnGnfLa5G35pPl3Z5+OqkxnMcV8cSGYAABQjSURBVNVHjQ8MVmvHuRqz4Zz93hfd/KD2VxtK7jXbi/KhXnSPOTPk7G6/0YbYvlEn5rDQPsfg8Yv3LbQP3tXuQ60Bv9/uN7eQRKoB+e+sTN6vcX2NNxkUhnFSBumh8Bqq7JUMjAxci9VRTpYkA7+NgR+UG2Uxb5tyr/HEv7X/t89/b1xo1zsG3CVcdT7uLuQO58+uOSY/LbnK59F+yftRpny75M3zkVffl4GM1e/rm0T2tQz8qNyQ3d4XL45+lP1fGyqHtL91oX0IQTZKBpKBZCAZSAaSgWQgGUgGfiEDudD+hU5Nk5KBZCAZSAaSgWQgGUgGvp6BXGh/vQ8SQTKQDCQDyUAykAwkA8nAL2QgF9q/0KlpUjKQDCQDyUAykAwkA8nA1zOQC+2v90GIgP8at38fatgxK5OBZOBHMpA5f8Bt+UaeAyRlk2QgGfgODORC+zt4IcKA93Dye2Cj9ln3SQbwjtZ//TrFT8LO7r+Hgas5r++aba/6wvXW3v3N77MtH8awd4H/BPL4HcR/+i1Ug7Ouj1lyU1ffWZzj3UBrFvx4BmzMOP76w3fkRC60f3wopQHvYGD4Otc7lKTMZODFDPjd8O35wM6vvCJUvtiIb9z01y/G8XJxYkd3o/ByHT9UoLyKTfx6ZczSPl/wCtkfSnfC/iEMlEU2BrwTr0B8R068dqGNHRR8BYy+phf6hndwtK/dgdgdhnxtyMrt61P+q0CFW2BpROPOpg5I7atF7IS2Y4x29YtX2CmYfRWww1IMtPaCc9vap0eBpWGHDqj3X+4y+/RdlmgIObgOSIWOQ3YME9jCjsBPn8FaPpNLfh95o69M0fvUV3Gh5Y2niq3yuodT+zY8eA982A9+WfjXySSutfwkzhBLEBPMA5pxmeIptlsc+viEL6ze9SP7RIfGofr3Q9/5GtVFMoG9P6q8gsFiGD50MmkcKRzc7g6rplgQ86I/lLk9TObtXr9g1/gJ+wlXAIDYwnVvdHctckvT/+7P7f6f1cpCapP/6kpbfoa2bbTwtpYnz4xnN+YFUtRPk5jwsWYxJmN9wU99mBLHJ8cg+KN+iAeBGGFxMiledN5pACBDLvdycyWT8xDUzcpQNzvqAmFWuSgzPCd2tMHpxH5RYzKPPzGZ2cplscwoBmd1VqYxBJvYzwvOzsxXHGsrG4qdq/EHuAauYYPliMm/Pe/3jZ5UoO2xb5GAdxkf5GmH5p3kFfAs8inK3/rkBPOHramWNOOpm+iCo6Af11FnrpN+B/sYjydygnVNzl+70G5JZvYc/LqQTGatEwYL/X691PHA2V0XUlq9DHimW2LCgrAEgFYyrhaEpAMYCl+Ercigdv21BKiqkH6UtIKz1DWH63X5gmaHU78CGeOc+NMVLe2QVg/5KHn9J1h4QFjaQVxAtnF8HetSX5kIO25AcBcHoy8oSdxuTYBTfNP8C/sMW9CP437w7x7XF3BKzGgcjvHrgoAvCmc3zbWyeLnd6gAU8Rn6PbZP1IPLMkEp7gpsWRfEJ5vUn5u84hSzNbIPn5RGbHFORrYHMgXHttUJQs5vN5lY7tVvQT/P0QnfNiLKeFgmQcobqWs5UPhpNtkY1LN4/Nryo/FNY14kxfzUxzLhFpxtLKx2UR37qNi3Hs+8nayvIpxiCX10cW6JZJa6RW5GRFKd2UGFB0/Fj2Uh1OXnqruN+12eSYcrubtnfyAzisFlnejTfK9WOptWhrfFn3YVORTzYawtbWh5rkLl2mLd4SLcXtdoQ8mZ5s9+bRSYJ3dKyg1iijF4vZxPHneRo2uZegOmJro5LELTyz9+81akFv9IbNM8G6mjurM5QV2H07cstPnOxYgddFtB4NgSLHT3VGVbEIoQbdMpw06D4tF6c14NQLsWeQiuem53U6rH4WlYyAYzzM6sb+dwtwis7aVthWq4ZjhN+vxsZYe0Njx1gNWFdmQH1UG2JeBFrCRzZoXJ9wN6j7+PC+ArMh3Ha5zGO8WA9l3383x2/o247mINi6HKQ6Qvqpux2Moa1xpLMvjQjYHmicb3GNvglf3S+0JjqalFH7+IrJWruj2ZKytNXttdbDnfy/PxIhNE5zf4neITsmF7LBP2jQuYuN9F3zZCRHYxWXDzogn2iL/bUyFtuyJzr5y42Wva14NLFxPASI2BUY59XHG+SD3HL7ft63QaaHpmWPo+Pl5kod38ilxRoWv/hTKD3CQ6wlOzI2xGlW2BJzYofqoOTtf2B3NLIA+Lu9nYJN167tS/UQxGdeXes9sYO8LBjsweJ4vs69SGctO4GH8aTo5t+KqXJ7owNoFqbcNAULk6ko2IKZarMlvsq+ggf2c+1H4rHKV8nU9ht76yzXN98Xh9PSdGWVbyloW2Edjd4Zje5Rkcqw0mztO6diLJKb8/RACinoMDiVzrmvOUfHOm1PMgwo9beWCHDj1ScGoZnUhwFl5E52wCnLXFXd8CJ3WZni7tEKy8sGCOd+yAosFPV7Hu6Fv6kDEDFB0dPtd27Xv1ES+Ate+6n6jVvr1/I65ZjwhRXeWi7n5OfR9jIRr8qXJdBxONRzlxun03vnK8SsWOfdLE+vg8W9YdkMmY+HwZ86F9I64ZH2ZH0xjKrDEhk6n0u/NCMex30bcNksYhx6TUkc7Hoz7L4rbM4eFzjafDPbShcUncE0Y0VIyPrW0+oIZs2okXlVG6jnPSUSyk2S9oHA+B/yb2qUyVMclNbRSfmB1xu6G28FdvHGzuHlq5guW4vOMLJ4QvIvsjmdqPhbXzqK40sdhz9kxEadGOzGWsRTZg7lQlFNvllDYWSb/TJeXl5yfUtvSdr41Y1XBOOhBTzI/TW24Sms5JfHNbPi832LRrP2DQgiCftM2xE9hyqHXx17mciOS+eaEtk037nXKEgupGMmTg6e72qH2ZWNvowOfShINjXGjfSK4lHImupxR0NTjWWPrX7wke3LVykEm5DWijbuNA6g7iHIB3BWwHn5eFkOGUXpEdkGoYUXIda6Qv9GEQFw6fGwACnPS7VvQ3vwX9ukWN8+8u1xRPR3GWgflCXHRYiud4IR/wCS+DF1z7vKq7yIj52pbzVzi8l65RXSRT9R45cfYyjr5zXdwAt9S6uGvNB9vLJEP+68SifX+Mx5E4zjoVw6XFa7sJwkDjYqt2c23bpHz2EWuUuwM4FGjMSYHFhD+vjcFdqYMtTY76yPnZx6A07e3EnFRlc1x0WIJ8UN1VgT5qrzascpN1NSNw6GwoxY4nNFwfjat1m1mN2jLDMOvQ5wf34/PJ3LIQV2/YO//KzWHZPNuRGcVgVCdYSmzc7acSS3xUEclcxVo8psXjj/qnAtZYc7oaR9yW10N8TqbMT4lvxBTLdXoLh1jjcf5U0ehfoeNJfa1DHs5BoPTqeCic0k2HxBJvcEL84qj2EheLpoeKX7vQFmPwKA3Hg8aJ87gvT3ol4SCvHOvkZn3kugaryJC+UR1+e4O8xnW/I67l/Eedg4000YpTGCcUaJ/meLRr3BjWegcF26EfYnDd49zztPYjO0riNazlaQD9kWEZFGZ2tIFp5ifouIQVfEBnE2K8jP4tNiuveIxbfcG2MVbhbQ8n6rWfLgz93a22E6yKY+5fxsNcc7nqEw52cEL3Oa4tPzDgGL/txk/t8HwK19xWsCJGpY7tYPs8TtI/2OfrIpnF7wf+B90O69K+OkFwH86xyHbzPXNW7RGOlJvbvXFouz/O521RBwznfNsIUftsglH9XW5ZOdo2H0DxAY5Lk0Xurrr3XCoHTW9fv4qz0o+wmj1tBw/jmXIC/9hvPD3XYwzOfcu5MI5LXmZd9DusAx4vY5mbK0LbYlZ5LH6u42DQxVeRD4lS34auzEceO3y19AXJ8KfE/WROFEyhTMLvuBYlUV0BIbqRAx7V8molc/CtxZrIWtuwHn/WXN+fG3K6HTH21j9Kxnpq7qOlbdN4arkjvtmx0fDWPoiJvX4rPLv5tOoo5c5P1318JCciGFL32oX2nrasTwa+igFJuhMZw3fi/xTySZz/FNuvVTbuxPxaU1eGlUnp5GS0khWUy0Q8pGHGfMBYVr2FAcTc5EnPW/SFQnP8Cen5BZW50P4FTkwTXshAd8c+LApeqCpFfQ8GsGsiu2F/1t8S93/W+O8Rh4niHzJQbixl1/Xk7v8bIOb48wZSv5nIXGh/M4cknGQgGUgGkoFkIBlIBpKB38FALrR/hx/TimQgGUgGkoFkIBlIBpKBb8ZALrS/mUMSTjKQDCQDyUAykAwkA8nA72AgF9q/w49pRTKQDCQDyUAykAwkA8nAN2MgF9rfzCEJJxn4sQzgL/l/rAHfGzi/saN/l+/3Rp7okoFkIBn4uwzkQvvv+j4tTwY+zQC/G/ZPv7Xj00weEKBvSjjxyWx9i057dR+ut62+h7e9txjayxsQShm925jf15tvJgFVeUwGkoFk4BADudA+RFM2SgaSgYEBWfh1C7WhTRZ8OQN+J3x7PvDkQd4hLF+erV9kLx+jcNc7X238csMSQDKQDCQDP4CB1y60sVvSvrSE3S4dyBeE6Hsk0RBy5Jp3cXRnhT6s4OqpHDK0j7wzU+ptpwbq7KtF1H+GFTJbx94+91WkQwuQHSyP7kuTxRbCuLAduOpXxkxH+UrTGRv4i1lBv9B/w1cFCf+M41ZWZfq2XBZzbTbXr2ThE7EifFaHMtNn8q1sChe8uDir72MueG9390UwxNweZ1Nd+GrXQqb0Mdz+q2Tebv/VrghnKFMWatvmvoYK+wr+RXyGOa18Vt4Ry5Dr7OP4XBHGX2Trdmrx1bKVzJAXZ1vls44vFUgoc3tYTNzu9WulbbwI+0mMgQjwhOvAfpFZmv13f273/6wl/NdkyM9Rto0W3rnQNq7yLBlIBpKBiwy8dqHdJvoybstEsD3KxL8/F/CXkdqiBwtVmdB0Iqgvl9fv0JdFEy2EyuTnX0DPX/jTfiQTvGkdChZH166X85APwdd/MrlhIl+IQkO1D+1UB8mHHVq3YzvaF5kkR65NRvtMKRwk7cC7NOyul/36CVkWBJDTyehlwubhWPrdjJu2+2YLjTXXskCCSXVRZzGyqtPFCAFx9lJ5f+raCW5V3mLZXQNLEPO9AncdyRTnrnlxYsqiHblyTWZdFMIekS5ycM3nLZbwcQjiCHHKHKov+jHkaiw5W8/EfMBLZEOAU+zdtrpglvPbTT5nf39uki9Bv8ItcqrwTDnWO7a7rn7CRgNVSk7d/3sWHzR7lPvSrItR1U8y8jQZSAaSgWQgZOAtC235rea5Ly7ZgC47WNvDrsvk0xYqw6TcJgq20E8UzzqJtAY8mVc9rYImTZY1O8cOW7WRdpjK/H17avmHTKC0ezQT1sqWWAjXWdvRXlSUnTld7MlCGztw7djqbELmeiyc1v14EVBtMf/tyVzS0mxXebJIawsv6dPLVa6Js0F2UNfLE0o4XgZZVODaOR2yUMNitnXQmDWO1MZDC5lIZsBLU19ioe2+K2dl4bbCuZYpnJmMzj6104iS9iXUiCPEKXNovvCYrHwen6ZpPIMeqeF8iGUGXAc2xDIrNvUD+TzudzVeqv+Ud9InT/KK/9ruuLQRDKVtgWk6OcdHdrMkGUgGkoFkYMXAWxbaZaCWwZsH9RWCUt4GdF1I8QBvHXmyrN3aRGFNuolivdDmiYMneRI1PXVtabKtO6e0MMAkNpXSF5q9Tj41O2s7L6bL432bPf0Ckm3YweywcT/saM/8tyOTTPSnKr/uKmpMyYnU8QKWdWg/L65cBXVugSHtys8z7CZjIk2LdnnRluVxQlucHot57lrPLVa0DvZHvGhjO7E3V1yU+dhoUdbkAguOpm7ITaka4rrdRKm/eQyZyCTx4ekyH0KZAS+kbbAhlFkXs7LAlX53vlkJ+12NF794dnFO+h6P+izO1bt8mXBBHORpMpAMJAPJwJyB9y20y5qCHuHP9bdSGcRvtPs3H9SHCQ0LPJLdt+mvqWmd+O/8qJ9r5+fLRZWblOqu2bDbNxdZSssEF2AZ7Rg5Gts0hR22pQ2znU3CHPZb+m+yK0gyl6cd5tIOC/muTnYHmWtbQFbpsshC/aputsBw9i6BdjvfDlu9SYBuEWEyj8X8qDaQ6XTvx6DD0j2B0bpQ5uO50Q3caN/dwZ/F56yMfVF3+yHmYiyhO47OpkhmwDVkTW8WIpl2cwHbcSw3/3wDSTrqxsD+GOm6tAvmk58Q6o42deK2fM4bE2gu9fmmGbCRx2QgGUgG5gy8dqEtC6HyWLrtBMqExr/XnWOoj3I/bFGuj1XbJI4BHT/L4IXLsk6x1MfM3MdgyIR4bNdS+pgu2bmuk7Bggmy3a3Y7OwnNsZjO0Y6oDjYqlw2n9ZnbYH8YisfzdZc+6gcdWHPh2n5PjbjwMoFxPBq3eCpi+muchFwj7tpPJBRHdaL7471aR/rws4rmP/4DtxHnXkzUmyHlQ2Q3klC25GymrJStZUr1kpeeE8KCRRQwlTwDsEhmV9f3Y59xngjOZZ3m7WIM0fqjseSJZBuRt6uY3+NlaUN1hPsZWf0pXY0z0at+ut0bF83ehX3ADbfgGvHkraQrlWfjnOru8sPK/U/gil+7tqIB9gMTac3TZCAZSAaSgcbAaxfaP4VW7GjRo9Mvg/6dsHwZCb9V8fjU4fOW/hSZn7f06yW8g+uvt+oIAttlp9YYq6goT5OBZCAZSAZiBv7uQrvs0NBvqmOe3lerO43fAMv7rPyTknXXkZ7WfJaInyLzs3Z+h/7v4Po72HUEQy60j7CUbZKBZCAZ2Gfgby6093nJFslAMpAMJAPJQDKQDCQDycCnGMiF9qfoy87JQDKQDCQDyUAykAwkA8nAnIFcaM95ydJkIBlIBpKBZCAZSAaSgWTgUwz8D37YwNv/zbm0AAAAAElFTkSuQmCC[/img]
| Цитата |
|---|
Natalia пишет:
А если марка стали 345, то расход на материал 13%. Как с этим быть? |
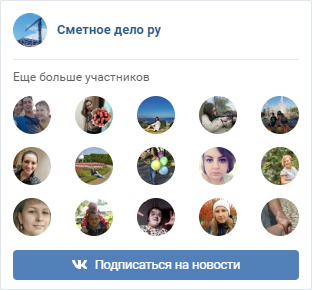
Вы имеете ввиду коэфф. из тех части [img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAo4AAABTCAYAAAARMYY4AAAgAElEQVR4Ae1dTa8mx1V+fwfiH1jyAg8RGi/ZGEVsZkXki4giNJtZ3i2RMluDxB0JCQRKGIUxMUNgQJFGXoQIRThYwkYhLPDH2LIi+85YCdH1fMQGFoVOdZ/uU6eru6u6n67b/fa5Uqs/quqp55w6VfXc6re7DxcXF463V+//u/v54y/ch4+eJW0fPHrmeBsv89R9+Gho+3v3lcOX3NffjOVhPvfcVw6/4b7+Jp9P3RPO19y3Ruxk23L3474IeX/rdw/uK9955j78NLY9dR9+KrdYnvraoD2tza091bVvUjtG6x6oqy//IIfQ7qif+nA/rTgST94Cf3XqHYqnMO2DR08dbU8//z/33e//xO+bWBW+/5s733X3fuVXfXu8+mu/7mh78ycf9LTbsK0yjtv2oP7Uxnh4ve1rc65HfR74Tve/YTt68VQ73vjNF91HZ99wP375y8kb5X/5uee6Y1GA/dR98Gm7BTFB+QLb+s5bn7f5q5jg2KB9m9aHk3Zdth8KMxenwyHw6YR+v2B57u+ynek41+bk/ChbfOzp/tR/LmOtOk6Lp2S7kvrCMnXKeMs9htkn5g6OqWC86PhHt9Uyvplln4hVton3gW2Ur2Nf3jXShqQR79696w4sGmn/7e/9m/v5Z1/4SbQbxGIgffjUPRjdnrkHD+PbBw+fuXZ76j54SFs9mf+IzyP7R+2EP8ivFgL9eQjna+6bTT4xKQfcJM/48aCNQlhXnUX4sKlbc4nk8f6J+CPrel1P0G5/736H/BBcS2lbfJ4qBiK2N37KTRuKlTbtwaOnjreLZ//r/vGH/+VoH4ud12rhSGn/+h8PvHD8y9/67WjeWHl5jf9J6vYjapMvuT/4UeXjxi8pbT3JVyL2O/Gq07ptQL6TdvUde+F4+8z9+MbL7sc3vpywvew+un3mhWN3okmrs49L9zrHQ23v0Bgw6iPtM3Ge0obJeeLjUTuuivSAcxvvHPc5+9B3wragDlF3ry/Tx7NuH4nZ8Mw9eNTdurEjOPdy0/y7XD0nMXaM+TD024z4TY6PLuessWRWPdp/A+c6bnLO+zgmjknz2kTEUTLnjHZXtlG8Ne3n7ZtSP5UROBKTjwdsIW1IGrEjHL/1D2/6FcdoR11cXIQTZpxDSh4hajI6tu/4D5+69xO2ODdRb8RXS+ESlzHsKXwfPHzi0rZhu6fVfTmY//3kf9zrbz5wtJe82b/f+avvuj/7vd9v/M3ntJf57bjbfiQcb5/ecB+9dtsLQhKFg9trt93tGze8cFzen5njSqR/L8+x69PcOjmOx/a5uGvJP2YXp6+F7zZ5PHHvPxzeqnljfrxu0z/HazetOJJG7AjHv/i7H7mff/Z5f2CcP3UPcraEAZY7c/L+/Kl7P2cbCfKmE5w/ce+fP3EPEjbKl7WlcqB8HjvDxgTh6H2b0W7evxm4We2RyKPCZH+k7DN85uOni/npxRfuB29/5Gjftm9OzKeK7W7dbX19aTn29WH0Xc/Bnp73xosvunZ7zt148Tn38guR7bnnvGCk29Rxv+RwWKhPZ48B4//gJY+B3DdzxkHKmzoeZ+EOi4hmfA3GwAV8wT5J2WfZR7HW128i11PqXzpPDt8sX0TsHagrZS6lPN6/qT7J4psZZ1nYuXGfySXJHxkc2M8Ze91+pA1JI3aE45/+7RvuZ5994d47f6q2J+6982nbWKdbCjesd3iimcqByoX1hOdzcHPKDnHIScupcywv1TuWZ5l0Hbv951rwnv/ic/cvP/nY0T5XuE61Zax9puJSuTHsnPSQR79Pq7GjbfuxOkLcttzg9U+euPcyNt3O3fN0Xw3ySoj5MX8skT6Xc2r5Ie6pGLF8Q7i5aSF+ehyH5cbjdIhXF2uMR2r6OK9u3VxmrA7Ol7cf8gOlhXzyOAxhh7hUzxC25jHtfIgPOq1r3zTOYzhyrCRtSBqxIxz/5LUfVsIxdVDWDZ9abiyfxl3D+RjnnHRtT07ZobxZuI/de5+027ufPHGQ7fyJe3dgGwvUHEEAy1v7jR5C+s+PfuEf4oJgZ7XHmBhq2+q988cu2EQ7yjZNOx6rdyAdap+oZyncob6TkDbYPwZiXvcH3QcGcTP6pcadE8MBJ22b4jSnnqyyS8WFxlXnuv1SzzvtoXCzbE+Iz1XjaduXOkf6SXMU2EH/UP1BpxVrlwG+CA4kHEkjdoTjrb/+Z/ezx5+7dz95DNgiQuTjJ+7d3G2kUapGmsI3wi+prqFyxGMovU17h/yQmHcN+d755ImjLY1LZnt8/Ni9u+QGiedUm5SPcuO9Ny5S6+/Lp3g1bRnJ79sis682eFxPBLdoO0ypn7nrfSIW+a2ojZqnaLNOe3TzvvPJY0dbWp+usaO4S9nd5dzMH1EekfzRfEvxjeEOcYrk9zE0VCYlLYLbG5cRvIwx652PHzvakmMo2h4RDrB8Ob6YmdePm+m+SJ5PG9wYvxzfRcozdsKetCFpxI5w/OM7P6iEYwIIB0zvvh6UeHCK7aeIhaC+hDra/E8ciTW9NQOR7ywjAibofFWDsaAa2k+xM7dMa2fVkdvzrs3aB8PnGm/meUqbNRNaJNCDNoi3V2t7Ctc+/6SUjeQZs68eaPM4RurROEG9lcgfiskmTeOkngf1VQKkEiEJbabbUJ73jT0yT30cG1Mg11J9gMzX489BeyLjWam+HIxPkbaBCGgRC/D+Amy7LF8Im4JyidfT/NA3psWuJ4wtQF9J/lPsl2Uk1qqPp/Tt1DILtU3rzzZmSDiSRuwIxz/69j+5n332uf8Poi14eYFlHMz3FgMWAxYDlxUDn7l3Ph7bLoub1Wv9wmKgZAyQNiSN2BGOf3j7+84284HFgMWAxYDFgMWAxYDFgMWAjoGOcHzr3Dnb9uGDP//e29bWFu+QGEDFEgqn5BiG4IzAKGkz1YXgjMDYq90I3yEwlvL/4RuH6NiE4IzAWMruPlwEZ8KgP/nRlynHJhx3LBwQgdgX5HZ9H/98cDujYgmFw7xK7BGcERglbJV1IDgjMCSnJY5JwPBG+AjOx4SxhM8JU/pc1rEW30lOJY5Rdptw3LHoQwQqIhARPAxj+yITFUsonJIxheCMwChpM9WF4IzAWNJuFi+2b8XzZfhCtjEiZhAYklOJYwRnwjDhaMIxupSfGsSIQEyty/JtXxwOtSEqllA4Q1zRaQjOCAy0XWN4CM4IjDGec9IvQyRZnV2RKtsQETMIDMmpxDGCM2GYcDThaMLRYmBWDKAGPMSgRlxQOCi7UnAk5xdeeMHlbmb3uv+pkkJOt1VuW1P+tWKkxHrJPOx3Xaf1N5c9xsi4M+FoomGWaJAdUHdOO1/3ZLa29kHFEgqnpH8kZxqgc/7kgF6SM6Ius7uawOe2NyJmEBiImEBikHCM4VnczYs7E44mHKMdK9bZYtdkB4yl2zUTj6kxgIolFE4qb0Q+yfkYJ/A+H5nd8yZw9isiZhAYzGfte4u7eXE3Jhy/+tWvjj51fZxPVb9x5p4/HNyhs113t0qKzTvXBYer7vSNMSFy3107IDkSnvRDiC074Ftr8VnJ9rG6Zv3jISeYIJakX31cybh7351eObjDlTN3T+arj3txInll/cPHOf0qllf3o7AvS84pE/hPf/pT99JLL7nXX3/d33Ii7hJj2JaxMaRcuuRsdvevO461N8J3KRiSIeW3uCvXVxB9GtXfhoQjiUbehl7Tc8TCUU5WzlXCSF2bNRmNBJ2fMNsJ5t7Nq+4wIApvnbDAA3J848xdu/l+Iw48BzFhy0CM+qcz6Y/YvKQ/DbtpR8QghMYIYkm2lYohH+cn93tt6cWRmBnHOf2qN2+sH4m+LDmPTeAsIm7cuOF++ctf7kY4mt397Y2ImTEMKRrpeC/C0eKuG3d9wpEFo9z3icd9CkeazK6cudNGrLUCzwsoIa7eolVDee4nQhZ5/SsnXqQFE2S10nLtzpD4iq12qPy6flpRlPyGJlU1icsJb1Q4zvGZ5DTEf2odNab0rRbJb53XK11+BXagvWsO7WrYhHIaQ8bQUJr0Ex3XdrUr58B/KnRdM8+DWJJY3oaKd7dNVGwvtvKW0K8azgl5hU161WZoAteT2F4mcLO7mrz72hsRM0MYVK/+24NwtLiLxx3FghaEWizqc51/v8LxcHAsNIIJLZjYI7fVZLo8biaeajLsE47PixXA7qpP4qQlheIAB40f2KknacIRqyi+rLzmjyf6TPpG85XnU+vwGFf9PwOV4Lvvrl2R587RalLj+yEhJ/mcTywXYKgYGkqTfqLjSF6OWd22l30+Khylz7Wd4rwXR+TJtzWhXzX443mDWFL9iCZkugVNt6Jp4uK/2CRGacc0gZvd09obETOEkfNncbe9r6bJsXFOzFCcaCHIQlFej13j9P0KRym+zmmyqFehxGRNQuvazWp1slmBEunhxK5WT2iiDIRYJSAa8dJMVLLc+KTVqVPyiWIyPmG3wo8mXxmI1eqWWtEibLahU0+GzyQvjSPP5bEvk1hHXe7WzevV70jvXFftpv0ax/WCJOAwsZzA6MTQUJr0Ex2LvNWKqVgp1Xkv+TyIJcmFbODf2QZ9juMy3PfiSMzsY92OYZ2hEO3P6//x8raE/URypgGdbkHTrWgWj32i8diEo9ld/bOQ296ImCGMnD/K35kDsvvVUD9aLs36W/UP59T+1iccWRTKPYlHec7HJhx9Z4kJCVq1OnP3gsnbueDWtU5THa+daNpb28MrRv2TVjO56Tr1ueJQlSNcseJW55EdECMce3wmOWm+8lwe+zKJ7cLlaH9CP0FQ7UbXWbw0e/GPQnOtbicWOHPKeYyIP5gr/bMSiy/tK8mNeck8KzkOYkly8j4koRWPwSau6zK9OBIz+zihXzWYCXkbm6rJUXLmCVwO6iQg+TeNenI/pgmcbDO7X/L/MOS0NyJmGEPHV9+5xd32Vxyn9jcqxwJw6t6EI00YciKoJ/bTEyEs5IRNK4n828U6b7Ma2Uw+sf+2EiYkP7mGqxl6Yg1XofSqVF+94UojY8oJL/AB2xHxS2NrJK3XZ4zHvpb+lD6Ux5xXrXhG6xDlmtuI4tpbQ34N8ml/DrTZULk6bYhrNE36ie0XvvL/iHDs6byXfB7EkuRCvpBtqFa9ORZ534sjMbOPB9qxg5WSl/K0q7+Ss5zAWUT1iQgawI9tApeTmdlN3gj/Yu2NiBmJEdYYP4vx4D649r31t2rc4JbNHWeo3FTByOVMOJ47F0zIfqI79IrDRpjQhKPEA6XFH1Tp3qaO502YtFSdwxwILy4aaXCQHTBXOOb4LBiIhvirtOQ6VDlfn7oWtJv/7WIt0FW+mD/lzwtunSSUI0xaKWSRJ+sYStMiRpbTcarzXvJ5EEuSi7e3/WfItykLSZmvPu7FieQN4mowPd6vUvsgcQ7uFKifoUjONoHzdDa8P0bhMmxxlRqzGxEzCIz0/hRboCh3zfpbKBxz447yswCcut+vcOy7BagmulZIqIccaKJSE3s4EdX563qCiad+6EKKTF9WcJJiJejQqs5BDn6Ca2+T89O5zEV2QI+jJ3TpC38ssMRKWKes5igndZ0mz6fWITG4rs61sD2ioi7SpuHT2D1iUJfzdrRiKWijoTTmznufV/hctw/nW8E+iCXJR9vLsd9jSy+OxMw47u9X3X+qevOOtIPkbBN4yjR2nCutKZabcJwvMK2/mXDsfZ9bIJYyJoqkcjQRSOGDxt8InuyAo34r4bMSdWykbUbbY2V2ZMXSAHcUzqj/gLEmOZMwyN2Iq8QY5T7gv5JlJedcm2MCqiT3OXWh7Ub4DoExxycly6L9X5L7nLpQdtuK49QBFDhpzAmEyy4rA3GUSwmflahjasxYucF/8rJiacCXKJyxeKbbz72r+gP8YrgIzgiMGLclryE4IzCWtDGGjeB8TBgxHy15bS2+W9LGGDbKbhOOmQN8rDH2fA0RiHv2n9ne3nZCxRIKp2TbIDgjMEraTHUhOCMw9mo3wncIjL36f6t2m3A04Ti4CjQW2FscNMZssvRWzJX0BSqWUDhbs93svpy4nRIniLY6JowpPpxTZi2+m2PDlLIou004mnBch3CkW8z8YI/9dnRWm0wZUNZQBjGokR0onJI+QXBGYJS0GdVWZvd0wYzwHQLD4m56G+b4DtFWhGHC0YTjLJGCCMSx16vkdAzLW2YAWsLPiFgiXiicJWzsw0RwRmD08VvqOoIzAmMp+/pwEZyPCaPPT0tdX4vvlrKvDxdltwlHE46XLBzpFTfti5D7At6ub1cQprYdYlCjulA4qbwR+RCcERgIW3IwEJwRGDmcEXkRnI8JA+HTHIy1+C6HMyIvym4TjiYcccKxfqL5lF5i7m87t4KwWlXk6+LThf4W9VX3/BVOa8v4jiJvYYsvbQTvNaQ2rOv2X6WRx5RG76L0t7/r9zDyS7X5fYDivOmcGkOfn8t3OgrOdb6uD6p3/vF7MHnfPpUbx6veC9ji0zm/Q7N692Xly7h/M+xdQT9ADGrUfiicJhYK+AbBGYFR0mZUW5nd0/+pRPgOgWFxN70Nc3yHaCvCMOFYYFLIadit5Q0CkUST+MqMFzOx3yv6fLUYkseByKOOVAmfRig1AlAJRSpXC7aucKzFU8NDvLTZ1y1esi1jQeJp/FpwNqJP8xr0gbKprpMEYRSP0gV+KxzjXzLx8RP4NNFeafslHQexNIMDCqdkX0RwRmCUtJnqQnBGYOzVboTvEBh79f9W7TbhOGOCKt3oa6wvGDS02PLfd25Xy1r+JJ6EcGxEHYvFvjQSQT1psm5xTOL12k31snYvxK67a1fE6p2OA4HheQfnWrQN8Or4ICYcB/A8r7YMC8dAaGruXnALv6fY28Eo8x9wGxMYEUF4QUyuwC5pY98xgjMCo4/fUtcRnBEYS9nXh4vgfEwYfX5a6vpafLeUfX24KLtNOG5kYukLhMu+HgRiIK5IeAhBxd9J5ienpQAMPh0nRKVYaavsbAVUdZtWrBbKupvj++4aidLmvBVDJLyaTwbGYoDKSF4Sw6fxrXXe9wha5YPOKirVPYTH3Dp5hO11nvB2tRCOQ7fkGX8F+yCWZvBB4ZTsWwjOCIySNlNdCM4IjL3ajfAdAmOv/t+q3SYcZ0xQpRt9jfUFg4YUV+RXL3ZqgUMisBFiQhxGhZUQYU2ZMSF6qH/H2N62Pj0ROHJVk7icnLnToRXHjtAV+J5zV7j59hnygY81IX6b2NMrjq3Ardqc0qvVUbniKL9T7m9nN76S/q1vdSfYe9nxFcRS4xvti/FzFE5JfyA4IzBK2kx1ITgjMPZqN8J3CIy9+n+rdptwnDFBlW70NdYXDBpKNPkVsPrBE3lcCcp2RSy47epF3f36gR0lsjorkEJEyLq9YBUrijJNCtVAzAqsWEwEGM4FnP2KXi0kVb7Abo+rbKrr6sWrf+fJv39k4cgrl7xqGtTj7Wf/ilXfHHtjPlj4WhBLM+pC4ZTsbwjOCIySNlNdCM4IjL3ajfAdAmOv/t+q3SYcZ0xQpRt9jfUFg4YXLHzrVq7QkSirVs3808RX6PeFLGx02pnzD7hwuwSYPat8lFcKNl9G5G3SKtHGYov8SUIsWLnjevW+wWCBWWPxrXd+MtvX3ecDKhsXjnydn7Zmjp4fY9d8m4eF2Kc+PebfGfZq+wucB7E0oz4UTsn+huCMwChpM9WF4IzA2KvdCN8hMPbq/63abcJxxgRVutHXWF8waHTEFYusHe3NB5Nf7xTE0ox+icIp2d8QnBEYJW2muhCcERh7tRvhOwTGXv2/VbtNOM6YoEo3+hrrCwYNE03hyqfFVpaIDGJphu9QOCX7G4IzAqOkzVQXgjMCY692I3yHwNir/7dqtwnHGRNU6UZfY31bHDTW6EfjhBER5MctxiSCMwKjdBwiOCMw9mo3wncIjL36f6t2m3A04Zi1KqQDfYuDhrbBztfxUwJULKFwSsYFgjMCo6TNVBeCMwJjr3YjfIfA2Kv/t2q3CUcTjiYcLQZmxQBq8ENNQCgclF0pOAjOCIwUrsg8CM4IDKRNKVgIzseEkeIzZJ61+A5pUwoWym4TjiYaZokGRCCmBLzlWceq4JLtgIolFM6StmpsBGcEhua19DmCMwJjaTs1PoLzMWFo/yx9vhbfLW2nxkfZTcLx7bffnrxdXFy4u3fvugMd8KbJ2vnxTvqIQLT4ON74yGlbVCyhcHK4z82L4IzAmGtHbnkEZwRGLu+5+RGcjwljrj9zy6/Fd7m85+ZH2W3C0VYccSuO9TsM2/cMOudfTF1/tcUf83sPDwfHL7XmdzCe0jsVfbp8xyN/gSaSFjzF3X1nYdjJ1HsXr1x1zwsu/P5E4tTLk2KltpHzN++ADLjUX2uRX6vpxJnmo95f2cl//OISMahRm6NwwvhZ1v8IzgiMkjaj2srsnh6bCN8hMCzuprdhju8QbUUYJhx3OEHnBNpY3iAQvXi66p5vBBN9K1qei87hBVgtEGsxxoJTik1+MTan+U/rMb4Qa1SmyRNpU/0i7dauSsD1lpU8CVfU2Xtcv+S7EZVZfISPIuVa3seXL4ilGbajcEr6GsEZgVHSZqoLwRmBsVe7Eb5DYOzV/1u124TjjAmqdKOvsb5g0KhF1a2b193pG9Wq27WbZ0JISrFDgk0IRxaDvj3EZ/KkUOtL6+SR9dAx4YkvyQRtPiIcvQgUK6Cyrp5jL2J77R7jo7nv5zyIpaCN8nyAwinZ3xCcERglbaa6EJwRGHu1G+E7BMZe/b9Vu004zpigSjf6GusLBg0WUrQ/OXOnJ2fuHl+r/RzeBk4Qjp3vUwuhR9j17ebmtnesPX2+POEY5UnYko+0rTmmVdau3UHbDfLJE0kBbsz2DV0LYmkGbxROSd8iOCMwStpMdSE4IzD2ajfCdwiMvfp/q3abcJwxQZVu9DXWFwwajXiqvgHtxZy45kVXs/I3sOIohZU89m0VWY30ecSqoG7TDoYUZ0KIcjkShzGelE5p/O1owuWV0vr49KRPDIs6B/mIfMxnJ/sglmbYjMIp2d8QnBEYJW2muhCcERh7tRvhOwTGXv2/VbtNOM6YoEo3+hrrCwYNKaTYr+KaX8WTousQF1lBvvr3gs1vEPtW/AKxp8VXJQ4bwcfc/L4rHIP6vchrRSn9VrJZ3RS2NQ/NSPtYVAb1EbchPpr7fs6DWOr4LN0PKJyS/Q3BGYFR0maqC8EZgbFXuxG+Q2Ds1f9btduE44wJqnSjr7G+YNCQQor9Glyj1cL66egr1/2DM/63kF6c8VPTB9d5qCRIF7ecA+xqlbNTlnmwWOP6WeBpYerzx3jWYk+KQVm/59jPrdt2NV6HT7pA6mJuu2wQS0275duEwinpXwRnBEZJm6kuBGcExl7tRvgOgbFX/2/VbhOOMyao0o2+xvogg4YUYNYes16PtMYYSeUEiSWQGEnljMqHsB2BgbInFQfBGYGRyheVD8H5mDBQfk3FWYvvUvmi8qHsNuFoQmWWUEEEYvBaG2uPWe2BGmAuAwcSSyYcNxU/iDZHYJSOdwTnY8LYq/+3arcJRxMqsyYaxOBVuvNYffm3f0v4DBVLKJwSNnMdCM4IDOZTao/gjMAoZS/Xg+B8TBjsl1L7tfiulL1cD8puE44mHE04WgzMigEelObuEYMacUDhzLUnpzyCMwIjhzMiL4IzAgNhSw4GgvMxYeT4DpF3Lb5D2JKDgbLbhKOJhlmiARGIOYFvede5WohoF1QsoXAQNqViIDgjMFL5ovIhOCMwUPak4iA4HxNGqt9Q+dbiO5Q9qTgouxHC8ZVXXnGHi4sLx1uqEZZv+yIAEYgWB9uPA0QbomIJhYOwKRUDwRmBkcoXlQ/BGYGBsicVB8H5mDBS/YbKtxbfoexJxUHZjRCOt1991YRjasMdWz5EIB6bT8yeaUIYFUsonJLtiOCMwChpM9WF4IzA2KvdCN8hMPbq/63abcLRblXjblX7dxmK9zHSOwr1ew/5vYX88m/yf6dc/T7E2Gt65DXxFRd6aTe/mJte0t28MDx4f2P7Iu/Ok9wSVx4zP7ZDp8XSD7J+5/wLxbm8jrca7/SE/dZy9OUaf4kXj3sM9R5Iwtfc9HnUF+KdlbouXV6ey2O2SV6j4xw/gEQESoxsdUAvzXtufQjRgcCYa0dueQTnY8LI9d/c/Gvx3Vw7csuj7DbhyJOe7ScJyCAQpXAgfwbnldBpBF3fF2DkC7mD8vUqlryWIByDL7301qm4yjq0HTotmn61/RThOX27Wp6r1TjCEwKrV2T6fK2oJLs6X8LR3NR5ry987Kv20Xbpc4XtBzB5zR9Lu0f8YMJxUv+TE0fQF32bqlhb4TUEZwSG9GOJYwTnY8Io4XNZx1p8JzmVOEbZTcKRf5o4dW+3qlc4IJcIQqojCEQpHEaFRuSb096PJGBqgaTxNOaocKQ6xNdcSMTxSqfGlufyWNep03rSb9287vxXce5cd9duim9aexvFhN7BExyDvMIv3g5pV0RUa16dMrqeJYTjmUv2g46lwHbhr4TrQUwm5C/VV4bqQXBGYAxxXCINwRmBsYRtQ5gIzseEMeSrJdLW4rslbBvCRNltwnEjE8tQMFxmWhCIWgTJc7na530uhArlE7dJm9vb+jp9JlBj1p8OjN6q1uV9HUKUyjrpmG8nx8r1pWlOzI/2J2fu9CRyC1nGHOdvroWCLrxdLbn3CEcplCU2HWt7WUTr9mAusTJL+cGEo604ctxl7oMxKLPsZY2dCM7HhFG6Hdbiu63abcJxIwNN6QBLrS/ogFKokF/luRchUuwIgSTznde/CdSCjFcL74jVu+wVR7FyperscGWBFLOjSattkJwEbnNrWFzr+FWn0TmLP7KPj/0t/BHhyL6TAjHgKv0vfOH7gBDy3Cdi3BgvSAP4wYSjCUeOu8x9MAZllu30x0LlEZyPCaN0O6zFd1u125X75EMAAAX2SURBVIRjoYGidICUqi/ogIGYUMJR/naRfC5XIFU5v8qmhSPloRUyKdJGhaNzjXir2/nWSS2eVJ2ThGOMk8alemPXOO5UWmM7i8B6RdVjNCuElcjr/MaRMXmvsHt94fPPEI5Uj24bVbePx9g15mrC0YSjiIWc8SsYgyZi5NSHyIvgfEwYCJ/mYKzFdzmcEXlRdptw3MhAgwiaJTCCQNTCIHberIaJ1S/K11ynp4uFuBPX/VPTEtOvyPHTyOG+eQgneJJYPFAicSgG5Lk8jqUNcdJldXkdb5Rf4DW3y30+Wsmr7bpy3T9k43836dNq8cjpLDAlfofLUJkJwpHrPtRPfMv65DFzil3jNBOOJhxFLOSMVcEYNBEjpz5EXgTnY8JA+DQHYy2+y+GMyIuy24TjRgYaRNAsgYEIxCV4bQZzRExtxg5AP0LFEgqnpO8RnBEYJW2muhCcERh7tRvhOwTGXv2/VbtNOAImvNKNv6b6tjhorMl/wUrnzmMRFUsonJJxguCMwChpM9WF4IzA2KvdCN8hMPbq/63abcJx55P13MDd4qAx12Yrrx+swZyjYgmFU7KdEZwRGCVtproQnBEYe7Ub4TsExl79v1W7TTiacJz126otDhqlO6vVlyYsUbGEwinZbgjOCIySNlNdCM4IjL3ajfAdAmOv/t+q3SYcTTiacLQYmBUDqMEPNQGhcFB2peAgOCMwUrgi8yA4IzCQNqVgITgfE0aKz5B51uI7pE0pWCi7TTiaaJglGhCBmBLwlidt1W7LfkLFEgqnpC8RnBEYJW2muhCcERh7tRvhOwTGXv2/VbtNOJpwNOFoMTArBlCDH2oCQuGg7ErBQXBGYKRwReZBcEZgIG1KwUJwPiaMFJ8h86zFd0ibUrBQdptwNNEwSzR0A1G9K1B+aaR571/9BRTyPb2OprnO7yw8c/c47Qp9to/f0SjKcXpTltPEuw+btMh7Bqm8fgm5yN+8S7JTj/g0IaUF74lkDuq9kIwhfcHHmscY5uHg2ndU1l/ZEVj0ku/wXZDbWansxtI07iiclIEYlQfBGYGBsicVB8EZgZHKF5UPwfmYMFB+TcVZi+9S+aLyoew24egn6mkTFKoxt4yjA9ELl87LqNXLpbVgE8IneD1NLSpZKPmvqjR5BzCF+OKy3sfBOxNrgct4kbSmrEyTx+fqyzQ5dnG9LDyb8zHMq+75Ju99/1Lw9rwqa8Lx7Vn/DF1Gf9T9aAoHBMaUeueUQXBGYMyxYUpZBOdjwpjiwzll1uK7OTZMKYuyGyEcX3nlFXe4uLhwvE0xyMpsU7yGgUirfeKLMCzKldh6i787/UbmytxQOZmWIBxJhF67Kb57HXAkUdmzehjk0/bSeV0uyKfsFGkdHt4O6cMu5q2b153/gsyd66EN7O+N7sNYmt4fUDglxyQEZwRGSZupLgRnBMZe7Ub4DoGxV/8vZbc7HKL/PCPaijAQwvHu3bsmHJcKgLXjBoFIgigmHOVKnBZ1QkR5W+W5PPblhIgawtR1sJBq8Gil7szda84jt8ybVb3ILW1Oo/LB7W26pS6Eo06T5fxxAg+PITCpHNV7QrfwlQ1s50b3QSzNsAGFs2Tfo4GdN6oHwRmBsaTNMWwEZwRGjNuS1xCcjwljSV/HsNfiuxg3xDU5tkg8lN0mHGdMULJB9nocBKIXUnK1rF416lwXApDSWFBRW8hzecxpLEyHMH2bqlvZXN7/ZlIJMZHmf1t5Xv92kG+5k0jl44AT2RGxN4IXs+v0JMKjs+IoVt5E3fSTgM63u73dIv/GzoNYmsEdhbNUn+ZB3fateDZfmC8sBpaJATmOIcZGwjDhOGOCkg2y12NEIO7Vd2Z3KHJRsYTCWap9bIJcZoI0v5pfLQa6MSDHMcTYSBgmHE04Rn8LIYNt6BgRiEP4lhaKq2P2ByqWUDhL+lpOcFQPgjMCY0mbY9gIzgiMGLclryE4HxPGkr6OYa/FdzFuiGs8vmgslN2LCEciZ5v5wGLAYsBiwGLAYsBiwGKgbAyQcFzS5yjh+P+mkHaLslracQAAAABJRU5ErkJggg==[/img] его не дадут вам