Добрый день
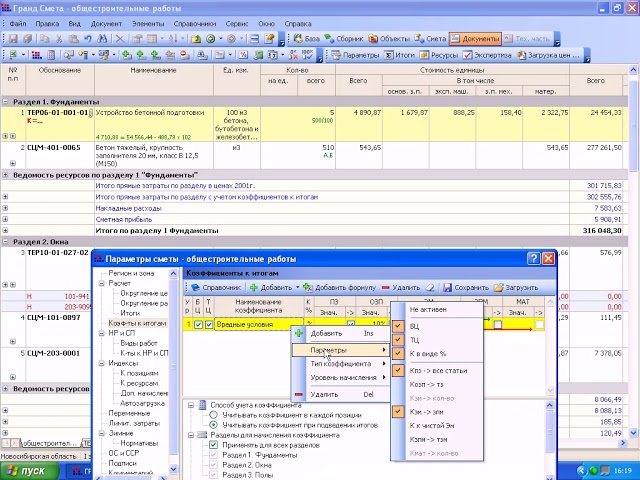
Необходимо применить расценку ФЕР01-02-127-01 из базы ФЕР2020 для сметы, составленной в ТЕР ХМАО.
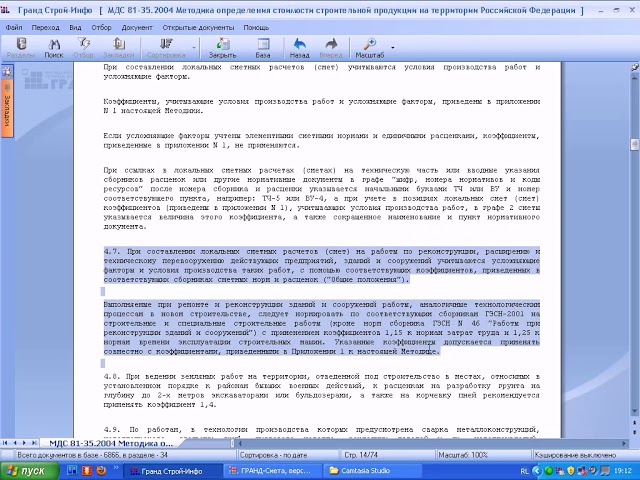
Подскажите, пожалуйста, какие именно коэффициенты необходимо применить для перевода? На что можно ссылаться (нормативка)?
Есть вариант применить ГЭСН, подскажите, пожалуйста, как правильно его применить, чтобы было актуально для моей ситуации.
Сметы разрабатывались в 2018 году, стоимость в смете базисная.
Являюсь новичком, ранее с данной ситуацией не приходилось сталкиваться.
Необходимо применить расценку ФЕР01-02-127-01 из базы ФЕР2020 для сметы, составленной в ТЕР ХМАО.
Подскажите, пожалуйста, какие именно коэффициенты необходимо применить для перевода? На что можно ссылаться (нормативка)?
Есть вариант применить ГЭСН, подскажите, пожалуйста, как правильно его применить, чтобы было актуально для моей ситуации.
Сметы разрабатывались в 2018 году, стоимость в смете базисная.
Являюсь новичком, ранее с данной ситуацией не приходилось сталкиваться.