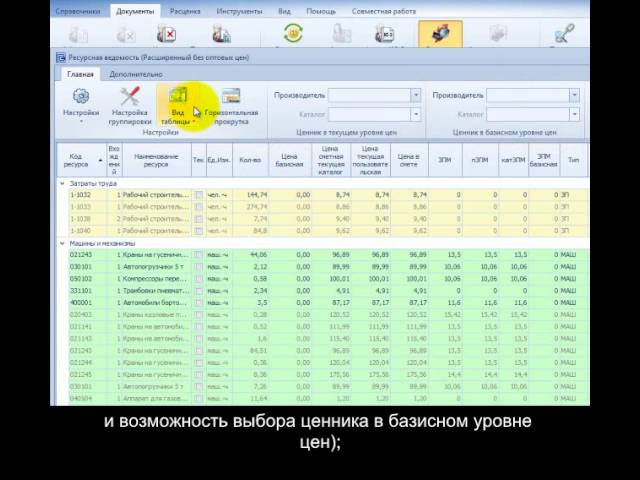
Добрый всем день! Какую расценку применять на демонтаж стяжки, по 46-му сборнику дорого получается, да и не совсем то
Какую расценку применять на демонтаж стяжки
 Участник Проживает: НовороссийскСообщений: Регистрация: 08.08.2016 | 11.01.2018 11:40:42 |
Похожие темы:Найти еще: демонтаж стяжки
Разборка цементно-песчаных и стяжек из штукатурного раствора на кровле
... Света. Думаю над расценкой над разборкой стяжек на кровле. Стяжки цементно-песчаные и стяжки из штукатурного раствора. Цементно-песчаную стяжку , например здесь [...]([...]советуют брать по 12-01-017-01 с К на демонтаж. Мне думается, что лучше все же взять 57-02-04 применительно, там хотя бы есть механизмы для разбора этой стяжки, ведь такую стяжку ...
... Света. Думаю над расценкой над разборкой стяжек на кровле. Стяжки цементно-песчаные и стяжки из штукатурного раствора. Цементно-песчаную стяжку , например здесь [...]([...]советуют брать по 12-01-017-01 с К на демонтаж. Мне думается, что лучше все же взять 57-02-04 применительно, там хотя бы есть механизмы для разбора этой стяжки, ведь такую стяжку ...
Разборка стяжки на кровле
Автор: Полина. Здравствуйте подскажите пожалуйста какую расценку применить на демонтаж цементно-песчаной стяжки на кровле?? по ферр 57-2-4 получается дорого и правильно ли это вообще? а еще сколько же см стяжки учтено этой расценкой на раборку??
Автор: Полина. Здравствуйте подскажите пожалуйста какую расценку применить на демонтаж цементно-песчаной стяжки на кровле?? по ферр 57-2-4 получается дорого и правильно ли это вообще? а еще сколько же см стяжки учтено этой расценкой на раборку??
Как расценить демонтаж гудрона при ремонте кровли
... демонтаже демонтируется рулонный материал и стяжка, с этими расценками вопросов нет. Однако, после рулонного материала на стяжке слой гудрона, стяжку демонтировать нужно после демонтажа гудрона. Как расценить эту работу? Какую расценку применить?
... демонтаже демонтируется рулонный материал и стяжка, с этими расценками вопросов нет. Однако, после рулонного материала на стяжке слой гудрона, стяжку демонтировать нужно после демонтажа гудрона. Как расценить эту работу? Какую расценку применить?
Расценка на демонтаж керамзитобетонной стяжки
Автор: Елена. Подскажите пожалуйста расценку на демонтаж керамзитобетонной стяжки 250мм с кровли?
Автор: Елена. Подскажите пожалуйста расценку на демонтаж керамзитобетонной стяжки 250мм с кровли?
Демонтаж стяжки 100 мм
Автор: Светлана. На мой взгляд. правильнее применить ФЕР 11-01-011-01 с к-ом на демонтаж. Т.к. у вас демонтаж стяжки - стяжка это не покрытие, а ФЕРр57-2-4 - разборка цементных покрытий
Автор: Светлана. На мой взгляд. правильнее применить ФЕР 11-01-011-01 с к-ом на демонтаж. Т.к. у вас демонтаж стяжки - стяжка это не покрытие, а ФЕРр57-2-4 - разборка цементных покрытий
11.01.2018 11:57:09
ТЕРр57-2-4
| |
12.01.2018 12:48:48
Дорогая расценка. МЭ применяет ТЕР11 с коэфф. демонтажа
| |
12.01.2018 13:01:22
Изменено: - 12.01.2018 13:03:06 | |||
12.01.2018 14:22:09
| |||
| Участник Проживает: НовороссийскСообщений: Регистрация: 08.08.2016 | 15.01.2018 08:52:07
В чем я ошибаюсь?
|
15.01.2018 09:02:53
ТЕРр57-2-4 Разборка покрытий полов: цементных толщиной 150 мм - по толщине не прорходит Берите по 11 сборнику с коэффициентом на демонтаж | |
15.01.2018 09:30:07
пунт 10.1 методики применения сметных норм [img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAYUAAACyCAYAAACtK9PpAAAgAElEQVR4Ae19/48c1ZXvp5/4A/xzCAkm3YM0npdIfjxQuhPZSZ5ZzYwfGq/CCESUsYLoXtaI6dXiRaCRUKQRiJgndSNYMhMRMSwINLZglOBuBW+CrbyeCMJaSTQevbh77SSs+dm7K2Wlt+jV07lVt+rUrVvVXd01Mz3dp6VW3y/nni+fe+uee29V14Ez4Kderzv/9z//05l9+K3Il8qpfuBPu+YUizWnrRlRHnDAv1Rv0LVrRQe6HEWnphk0yg5QdhqKX8MpMz5Fn0gLc5xGGY6tPKBwHMeQHapT1cWARxdas+245y9evMggaDu1oteXIRzdfiy7neqovqcMp4lLM+4qSeNDM6IC3s6W1+05HaXVGGP6ajr1G6OvQ/RwuPh4+TE8uB5J+mo74+hD5d51oq8n/3pk5dw+3raXtGPhw9slYWbS+fke8UniHWcTlftyOJFDE4Y7fqjeNu+wdjS3BH1N+up5ycKftTMkulkt11rZe+F/QQaff/+3f8XrPzimvteu/9pPU/mOfYo1tB0Hjv62FpEnYZtVFHI55HI5FNbn0dblxXnMKgIA03MoYwtXO9RgGiuah9PAVHUBdVXuad6pY3m1jKVFt3GnXlK8iX8pRBi2NEzXxPn1TWxWC27bQhWbpGepHm4kuR4QaGN700LWuYqtYg2np926/Ow8iqsbaFpIrUWdOkreuMnNrAJbV8GHQaQNG2c0FiqmoPwi1mpbmMkVsD6/Bm/4BGzi9O2cxzoCO/wGXB6NH6qI40F1Ifp1zK9510ecnSF6j78vHGhWljHZqKHIyigZV26Qdc32xCetvUn0pkZpaM22lI/D1TbvtIP+WZ5sY8Ubs6o/sYoZPQ7VPLENIo/9xMmNbdC9IhOn8Oc//wf0l0TqNP3u+oc7C+0QelaigElj1DfPVIHaaeh+yy+2fEfUilzpgaAw3TQWW8yBtWsokp6txaCBpHpDQF28zMH31iqZii6swjrm214fUf8ktwD4OGvXsLVcjziR/MRUNy691xvy0uk3j/VCBc0kO5P4NytYnlzDYsFQN67cIOuazYJPSH/P3q6CMyJIwjVOhNKXFqGF8IKC26EWqyv+3BNh1Y/cCJNoQSZOgbN9f+1veHY4080NrGoP3qwEnUKrtM0pTOgdhbFLGE5jxkurzvl1YH7W3RVy0/MTmNqs4oy3Yie6zfJc/AXF21Jajwda9FFbsz51vonKDNCw7T6JV5y++VnMI7AjUWwcj6RGae2kHcTGHCILoLjyJNm2ujR80tqbhj4Nrc2OXnDV847vXKexQguKmZJ7OmHoYBMTKetFbqRRcsEtydXdax9//HG8+OKLsYRUvyMftd2tMtZF1BrzLG8kQ/RlNBxvO12YxFYhh5xHXm443kTSQX2BdgntrhMLHRUVqu40UshV6Tg62BIaakh2MARcnAvIsa5fqM+iteheYCW/L6mPp9URi3uUEjSgPtKfQglqx7Y0lYMuL5bL3XcKofFURK3dQh76OLCJSk55BDV2phsbyBUqmHD4qi9GXwCLazUEdgDlWk2ra/zG8Ohc9Y6PtJ2uftO02ElrJ8po+OcbXHxcOaMJYQQfX6JQuK9Rqgc+PsuU9tLhcJtjycaEz1MnYnjr6qTf/CJix08IA2/e6ehxQouDRbTaUP29TfNGSF9arLgnCnqdGlIjSW6IMF0mR7cf0jXZh9S0zVoA1lIfJ+1DW0dQ5UuXLuHIkSPKslylCYdNUuSQF7AWXcn2goOMi15Qyp5mXHDfp3YOvFPIfsQIR0EgHgHuEIiK7t204smTa2iV1nfjZNZSm4CA4J4Azt5XjcdOYe9xFg0GQIDvFAZgI00FAUGgBwQyv9Hcg0whEQQEAUFAEBhSBHL0x6Ah1U3UEgQEAUFAENhlBG7B53dZoogTBAQBQUAQGFoE5PhoaLtGFBMEBAFBYPcREKew+5iLREFAEBAEhhYBcQpD2zWimCAgCAgCu4+AOIXdx3xkJN547RSO5o/63xcujYxpQ2DIh3ghfxSnXrsBXHoBR/OncO6PQ6CWqDDyCNzy2/O/xVdmv+IbSgPxPT/HEocfw5vr38atVESD9GGX6virF/GE+2fTUHnQ8hAe+/nL+PYXw+2CekDxgMfzgedxcfkeAHRRPKl0UfW3n8Opb72EK1wPn+Y4nu88AWqlPnH66Xq/nV8QJIj/qT/gIc8+XXFo6U28fPAt325djpA+fqmRCGzhFSG7eQUAJe+kQtuoifKKp/WaMjx8Zj3p7VMbiRs4N/8QXrqcpKfRRLIpEbgHDy4dwkPLD+GoNx7UNZSSi5ALAmkRiOwUnuhcxMXORby5dEjxogmH8he1Q6Dp+kLgNt57+RxumFJpYvf4XOx4DoHTePXPP8ALw+kbr71ud05hMmuuq364B73YCWbHy3yCpgmV7Hv1OHD5JTy09KFVj2ghOS8XX8JHOdMjTzCs3sRjh91WBw/aHILH0dfLpb+y/Gxvq8i+9TYs+eOv8MFlgPAJ4WKQSXYwBG49+bI/NgTnwbCU1r0jEHEKXZv+8RxefxvA4eM4ThPY5Q/wqx63tTeuX1fsD+W7PQf7Id5aBg55E2RXnTjBAPpxNj2lb78dynVe/QQ3/ngOp9hRijpWmbc4zCTGl95Sq2/afTyod18R+nvwhNpJUcWtuG2Cfq/gD3+IEMYXdNFbHVkAMI+HjuZfALm/Gx98gCvE/e0n/aOjo8xWs53mhySMdJ3Hx+dBDlfXMXx9ntxKdcwSHGfpoy19rOXz9Pj4PDT/HmX7thrtAlVoJ0V6uEc+plxXr3Cd0lHrv/Shj71ZHsjwdt4Mk57ttfbtUfSMU0imOyZCeklmXyOQ2inoCeHQzIN4cIamxCv44ANjr8AnC28iSYOS2iU88F18V014aVoGE1aifr2y9O2wn+cGWHzVPVYjvt5qXO20Lr+EZ+lM2P+8hyf1BRXZXdzAuZe9I7lT3jGd3y4moR0gDuH222NoLMUhvb/4bbzs717MncdBPPZzvnN8D68ze/QuUu34tK2XXsBDy1fULoJ2Q1R3Zfkhf8JR6iRi5E52igfRkQNM1NFioG0n2otexErTadmafTedNZ3lV6/49c6Yjg2jO+ig/8Ms4soZVR/2/kuH3Dod7bp95HPT9jOekf5jdcB1fNLjotCXIYmhRiClU7iBXzXcwfSNb9yKW7/xDbVSvtL4VfgIyRs06ngF7+FJYwJMPBrBL9Uu4bFH/DsEKQDsUb9eOWo7zCMwOjLKH/UnP9vW/taDB5WUK51/Adhx1cWOd0T09pPhidK2S9ArR+VIDMdEq1S6x0JSDn8DX6V7Nt0+MXoHK1n3PoFmc+vJJ/DVD9ybyTRJx927uOfYcdWEbNVHd8ePuf2n6967ED1iC2PkSSUd1f2c43ieHVnG6ah17fbbk14xsjnvWJ21s2c7Jt6ua/r6r/AHd98ZJo0rD1NFcj3Zi4O4zRg3PbXzFktPqhODHsdeREMpGFYE0jkFPXHhCl761lEc1ZPS5Zfwlu3JE35MAUCvThJXtW+/h/d6neRMVNPqZ7bvNe+tGtV9E/8op9fGt+KraocFXL+udxHBavA43yWE7jewezPkLDT2CE+eiVpY9KbJVk/4emXPeehVLu18aMVIRy56YuR0maUPP4bn1f2sYDHRTcedlN0Tbw9XvWOyXgtdGF1vAF8/5S4kOGlcOafZ9bS3WLLvhnddGxGYMQKpnIJeRehjA5pE9A1p20pQH1Ng4jbcig/xyx5XFqGJMYXBafVLwTo1qdZFrZgvveA+Wqi4hHczqkg7s8R7CZ4KtEPQT0apySh46kqvpv2z8h60dh21JryBT64G6XPzMefFR74O2hvoHSK31dwZ8DrNWf/G1X3+5HcVf7z9urqBHq+j5tT9t1e9TNkm5zidTbq0+SsTtwVPz7HGceWMxJpMtte7Fh/4ekRmcjurKCkcMQRu4Y+jJtvmDSQcAh0d6Y86Qlq+gitv/xIfHvNKaXtJDoA+NHEtw3u89BAeO9PlvLzbxKiOQF7ymOsfWlUCx5XMBP2W74lcBJqD9ZfZoY5Oogu5aDOu3wPPu08YXXLP1Y8uB+THX9Ur/w/xgn68l+8SAtL4FJdFK+yZeNK4mnuWn8fxt5/Ee/To4/Ih4+Y+3QMJnjSjvnxaPYV1K574+WO4/i06RnP7Qj1eq26OP4E3l67joeVgDBB26kkrffbM9dYY6TqlqPs45nvLV/DS6XN4cz1JxzjLjPIjPehlkf3VMx6fJJ0tdedeNuR3ybrHbb+MUMWVRwjNglh79SPNh2A9oo1tB0D3EbsugOP4Ln8yz9RD8vsOgdzFzj5/S6o+W6ctbeqjnAz7S+tBTpCdhWcoYf+z2o8Y7Ued9/9IEQv2EIFUx0d7qKeIFgQEAUFAENgFBPb/TmEXQBIRgoAgIAiMCwKyUxiXnhY7BQFBQBDoAYFbQI/Ry0cQEAQEAUFAEACQu3nzpoTjlKEgCAgCgoAgoBCQ4yMZCIKAICAICAI+AuIUfCgkIQgIAoKAICBOQcaAICAICAKCgI/ALX6KJdbW1lgunFxYWAgXZJS79sq9OPzURy63k2dxs6b/Hp2RgFFjc+0V3Hv49zh9swZUD+D87E0IZKPWyWKPILD7CEScAjmER//6r2M1eeXv/x7cMdx74AC8qRzASZy9WUPa6Vw5hHdP4PLN93FHrGSpCCFwx6M4ffIA7j/wGnD3c7hcC9VKRhAQBASBvhAY/PiIJqSbN3GTvmeB++99BddSqXINP3t3Emfff1QcQircgGM1D3fBLiVyQi4ICAJxCAzuFDjnY7M4+dHv8c8AaPV/4MAB73svXlGe4hpeuVeXHcC9VHjtZ3gX2zjj01ZxQfOkIxKznMruraLK+FSpgSoPHNKFKslxedl10UK8tr4cTz/t3GJ1sMjqUTdfstb5QpVhxeTret2A6EivuHJNR79Ek8YmW5tuGJj8VUdo2brPuVKSFgQEgWFHwOoU/v3f/hUn/upc5EvlSZ9rr5zBa3ffiS8BuOPR993dg9pBTOKpF2nmvgOPvu+tbi8/B7z7M3dX8dEkTnu7jcvPbeN+NblcQPXwU5g869IH5QA+2sadP9S7k5N47X7mSACQQ6Az9pveUZZdF8MSvuO5/BzuVtUJOnjNTVnddDOkutljNRcrkqv1iKz+L6B6/2uW5nHlcI+V9C6uV5u0/F7oNS3JIPrtTspdosUcKRIEBIE9RcDqFEij139wLPK1avrRUzjsrRgP030BPZnxlSpNZv6EcQFVoqebpJrWcyTE/46/OIG7XzuPC9c62L77OTzu3aDwy4no7hP4C33zgXYn2EaHtieeLmfuvBy+6Rqri9WioDBJhzhZXXTTuye9qA6EJacuVM/gzrPaWQW0ceUBhZFKsskgVdkketb3Bw6/ixM/9I4A73gU7998H4/qPrLxlTJBQBAYSgSsTuHPf/4PxH0jVvDVop7kaRKmSeJysCtwV97U+hhqamV5J87Q8c4deUyaTJmTMKsS80qXs5h86jD8STdRl0RuyZU2WUktOE6Xn8P2meD4KamZqrtQxZk7f4hHaQvGP3HlnCZN+p9/zx4a6KFhyKYTePdweMfWAwchEQQEgSFDwOoUMtGRrZiv/ezdhMnmS7gT7+Jn+u40TUyTedxBzuKjp6BOneiYmnicnI0+2XThPF4jWf6EeQw1mnTvZ2faPetiWN5VB4ssziKiG6/sMU2r8fOzeN9cdseVd2ObYNO1zjZA2HMeCfScLJRWOzOGf6hSMoKAIDDMCEQeSaXHTQf+nwI9Ljl5AIcPPKVsv/vkSfeMXq3an/IdxMmzN9Ukf+yHJ3Dv4QNQ1LT6fN89M6LJncoPKC70uOsx4FrHOyZyebuPwT6KO669EuBMxxeXodr+/uxNuy4BdULKnfStOuhWXNZzz8Xrpo5atM5347nL9Pgt01nzi/yexFnrHxDiyiMMjIIYmy5Ucfgp4LnL5gPFMfSRfnBtMlsbwiUrCAgCQ47A/nshHjmWvwJ+qI+qhgngYdZtmHASXQQBQWBoEdi546OhNVkUEwQEAUFAEIhDYP/tFOIskXJBQBAQBASBgRGQncLAEAoDQUAQEARGB4FbfvOb34yONWKJICAICAKCwEAI5BzHkchrA0EojXcagUuXLuHIkSM7LUb4CwKCAAA5PpJhIAgIAoKAIOAjIE7Bh0ISgoAgIAgIAuIUZAwIAoKAICAI+AhE/tHs16RIvPjii7HUjz/+eKQuLX2EgRQIAoKAICAI7AwCdKN5kE+9Xnc+++yz2C/V809aegB0Izz0LZbLTtEoA4pOrVEzystOgwu3phtOOcSr6NTajtOuFUMylQ5lC7d2WGaRGid+Gk65WHO6USWyGLPKixcvjpnFYq4gsHcIZH589F/v/btU3qsbPT0c5bRrKBZraFPacdA6PQmwvKJxWlgsIFzeAGZKdXS6alRGw+PtEJ88kF9sKVkubweNMlCcJAHGp72NqYarl+M0MFVdQD1GYKdeQi43g1WDhWQFAUFAEBgWBDJxCv/PcaC/ZJhO06/tY9abeVubvsqm51De3Ea7U0epVEGllEMu534rzRQcO3Usr5axRN7C/EyvYGVaFxYwWdTp6K9yNOTgolVS0iMCJe7kmxXkVL6DOuvbks0r0xjw+l6NAWqnxgVbNGh+ZjnPh/hU4A+jUHnO0wtAqLzkLRhcfYMx2EQlV0K96eqoy9UiwrPXXVDo8av5MNC4jlSsbWEkSpe468Cqp6m/Z1ecLLOc5bvqz/WU9J4ikIlTIAt0pLY7Dv53P51kWVr6CK/NKgrmRW4QderLWC1OQq3vN7cwueat6BtlrM6wCxqrmPF42SaU5pkqUDsNf+435PjZznmsYx6zFt/h00giIwSaqMzoPVceiy2vb9s1YP28fXeod5dWx8z5xanYRKVQ9XeG7doWZvQMTk0i/Il+G0t6F9qex/oCOaE8FpfKWN3wXEpzA6vlJW+nW8TWMtE0cWYd/gIitHNtTKF6xndHFmUTbLFeB3F6eqwjdnGRCbIYWTr9WUNJ7joCmTgFCtOpI7Vdu/5rPx0XvjMtvRUVPVD1BddahJqLmbMorM+jrcuLbLKmHQS2cFUd80xjRfOwHf8YuwS+4gk7ELqw1jG/5uoRT2e1RgpTItCsLGOywXddtNrOIUeTsO7zFDwj/Ng4yhWq2CRenavYKtZw2lsd5GfnUVzdCHYLpjyiZwsOxYd2rkRHY9Br29xYRXlOLznmsTS/joXSBiaX5gOOfCVPznDrqt3xqU2CiU3ABrbroJmgJ2tqS/aEGzVMob9NjpTtHgKZOAUepY1UN/OmOWa9mTfpU+W5s0g9OUSPf8xdAl/xtPzjJJqQljHZdu9HkL52ulSWCHEcAs0KlifX3JW1T+M59/YklnN8F+gRtLfdid2nZwkbPz6OrDsL1p6Scfw5H7X4WPF2nNOYK69io9nExmoZvk8AUFhcwtTUXGAfTai04GgHu6HYI0ibLYaq1mycnnF2ERObLM5H45ZGf6tyUribCGTiFLjC76/9Dc92Tael78qwFwLarusVU7MC/wSAjn82pzChj3+MXYKVtVoBhR2ClU4Ks0GAVvAbcwgccm9sO1e3gKkJdzfJm6Thl5/A1GYV+uSmc34dm+U5Nclb+Rv0XCylp0/XsDUzg63I0eQ0VoIbVW4zPV5p0U1yTWaUT2ML0evrYDpsF2dttasfWb3ozwVLes8QGPh/CvQ/hDT/O0hLH4uM2t5XWXURtQbbbrMalQzR09NG3nFTYRJbhRxyHn254XgruQ7qC3QvoZ14L8G9QDexWchBa1Osta2TFh0pFaru5VzIVUGyzGvfVFvyJgJlNEzQ1ErUO+IBFK76MEa1blZQUF0ZKvUYW/iZIv38NFbaNZT88ULjaFqtmO38TXrvvoPeweZnMV9cR9ebUPlFLE3lQGOGPsVy2b/X4KumEj3YEnMdhO3y9Fzazga3nvUPWyO5vUFgPF6IR5PGArCmL8a9wVqk9onAyL4Qj54QWp4M7nv1iU/PzeQ66BmqcSYceKcwzuCJ7YLAIAioG8xLTvRIaxCm0lYQGBCB8dgpDAiSNN9bBEZ2p7C3sIp0QcCKQOY3mq1SpFAQEAQEAUFgXyCQo/fK7AtNRUlBQBAQBASBHUdAjo92HGIRMCgCcnw0KILSXhDoHQE5PuodK6EUBAQBQWDkERCnMPJdLAYKAoKAINA7AuIUesdKKAUBQUAQGHkEMvmfQpp/NBOiaelHvhfEQEFAEBAEhgWBQeP7pI2klpbejLpG+X0ZeS11hLZBe2Z02kvktdHpS7Fk+BHI/PioWyQ10xl2ox+ZyGspIrSZGEleEBAEBIHdQiATp2BGTjPzpjFmvZk36fvOD1PktRQR2vq2dwwa9hV5Tb3JVkct8351BDezLikiG72riAd2orSVj/fqbuKt69Wbpkm28VpvU343ntTHZpsknU1a4k+vBTZ08yO1meU6r3/1GOOR3aiO46JsduNb+DFHFI0XMc5Kb9rFMbRETUzSx8fa0tesP3wMTF7aRr88wRZNO0K/mTgFwiNtJLW09BHM1dse2YXOO9sjHtrIaxKhLdKd6Qt4xK8eIq/Z3vOvheo6/f5/Xa5+mZzpFTduN9HpNuoli10isnmT1MYcxUPQ8RSYEM2L4i34OnThqdv49IwfmM5UrGk1/0iAHoOes7KmLfRahq+P+4ZYVM+gCXrjMMWDCOKN+Dr59An2WqPFccVMfTq4ulVEjeJP+Pw5fdp0F1vSshty+kycQtpIamnprRjqQaijpuk3oDJnMZyR18IR2qy2SWFXBCIRv2gipNVqn5HX4gRG5VgokyKyeeNxebKd7jXpSTwtKvCiiM7smsix6IC6TTJ98EryWHpdYf7mF7FGIUtzBazPr8GPSWXSUT7JXhaLQUWso6iJKnydyyiiP9rYtgac8GJO6F2NjqhHbDhGuVwQY0XrmsYW3Waf/mbiFMzIaWbexMasN/Mmfao8dxbaUfTMYKcjr0UjtPWsmhAGCNgifqFL5LWgdTiVNrJYuHX3nBqPDUxVC9GJpntrO0Vanfk1QXGiC+wIy4ZliJ6HPFVbnmjUuwR98hNTURsS6KPEXUps+isHw8LvchZxthnlbpxs3hCw2hImGYlcJk6BI5E2klpaei6r77SOOEUR1nYr8po6R5UIbX33mW5IK7o+Iq/p5uZvJpHFjAhrPCKbK889ftia8c7UTSVs+QSemehMMtNiGUMfq486xgIaRuxzK32CvSF49LVbiNef8Mf8bMavJKcjqqgtId1GJDPw/xTSRlJLSx+Ls9ru6VhnRDXckdfSRGiLtVkqKK5a+shrcbjtdES2ztVAcn4RrTZU1LbtniLumVHbukV5I1EWbKg4dK3QWXsL06hjOY4+0NpIWfjHYki7YjWLqsiF040N5AoVTDSAGWsUvBh7CcOQ/l7UxE7dbq/Sh86OCvAC1SkbFuqzaM0a5vBsSIaLUR4kgz4xttjuD3kt9vPPeLwQj1bpEnlt345TeSHevu26wRVPe+3SU1Ebc3BYyFYKg7uANWuI3MEVHD0OA+8URg8SsUgQEAT2LQL0hJgRiju/2EJr3xq0+4qPx05h93EViRkiIDuFDMEUVoJAFwQyv9HcRZ5UCwKCgCAgCAwxAhJ5bYg7R1QTBAQBQWC3EZDjo91GXOSlRkCOj1JDJg0Egb4RkOOjvqGThoKAICAIjB4C4hRGr0/FIkFAEBAE+kZAnELf0ElDQUAQEARGD4FM/qeQNpJaWvrRg10sEgQEAUFgSBEYNA5Q2khqaelHJvKa03DKgOPbU24MCv3YtJfIa2PT1WLoECCQ+fFRt0hqpm/sRj8ykdeaG/Q2Lfd9/E4bta1l1DsmGpIXBAQBQWBvEcjEKZiR08y8aaJZb+ZN+r7zQxt5jd73PoUJekurfFIhwCOZ+dHCKIhLKQi45Ef70pz9CFpuQbPCIqCpt9fqtiwyWMkS7UsFByux6GuMnr2Dn961oyKyGXJ9fc1ynrfpo9T24kV4sQAq9ZiobpwXtfMjpLntfWyUHOOtrSHZHiY6eJVZR+VxsnYiQp3uS/ndcQQycQqkZdpIamnpI0iotxrqi5mFRWSEwxd5TU9eG5gb0TcsMvh3OMmjbfUQec3ThhxCEAGNAh5tY0kHaqJYAwt1qA1cTLQveo+O2r1Sm8YUqmeaLudiEe47+Js4s07v7DU/XF+zTufj9KFx475xVMteYW/8DNukedEvl9lj9DAjrkDIDl1njWbGZO1UhDpumqR3DIFMnELaSGpp6a3W6wGqL2gdUIc5i+GLvKYnrzls5IxVmtVIKYxDIBpty1tJx0Ve88ZFKAIaBWPBKmZ4JK7NbaigXrZoX+Qt+Ip5ZhXwQ1vOY2l+HQulDUwuzUfUDumrYgd4cjhlnD4qfGsNp40XveloYSGbGL+QTCrfwehhEVlMDz+ZFF3N1j9+Q0nsJgKZOAUzcpqZNw0y6828SZ8qz52FdhQ9M9jpyGtakWnMlTexzUIK6hr57QEBW7StbpHX1LiwREDj40UtMCwxlLVK7TpKFM6SYv8SrbFiLiwuYWpqDosUAIZ/IvpOY4XiCnBnpOnT6BNnE/GKyHQF9B09LClaWowsbVJPv0m29MRAiLJCIBOnwJVJG0ktLT2X1XdaR2/axchrnXqF3VhuYmO1iElz8ujboDFqSCvKviOvGRHQjGhfsSjq8UL9xXYQbuAk3moaK+w9/qomTl99xMKdS5w++VnMowp9UsUlgpxhu4ZQVLc4mTGR0ML87DlrtDQijZVl4WPYl0mEOosYKRoMgYH/p5A2klpa+ljzaDDy0EpDHnktPwFUCznoWHHlhpMcyDzW8HGvsET/oiMdFoSdsDVPWnzUzAho7ZqKhpbTBLRiXTOjlXnRvgAsTeX8cVcsly33DjQj/WvRV1dFfs3oY6nv1xUAABZlSURBVOSEami3FrG4FtazXKsFrblNqtwmc4DoYbHR1UgFm6xAtXDKtM+LJjdQhLqwBMkNjsB4vBCPJg2JvDb4aNkjDrv+QjwZL3vU0yJ2GBDI/PhoGIwSHQQBQUAQEAT6Q2A8dgr9YSOthgSBXd8pDIndooYgsBcIyE5hL1AXmYKAICAIDCkCEnltSDtG1BIEBAFBYC8QyH38qUMvaZOPIDC0CFz+p8s4/N8OD61+opggMEoIyPHRKPWm2CIICAKCwIAIiFMYEEBpLggIAoLAKCEgTmGUelNsEQQEAUFgQAQG/kczyW+dfTFWjdL9j0fq0tJHGEiBICAICAKCwI4gMLBToAn+1KlTscq9/PKL4I4hLf1dn/NfQODL+PJ3ysAbq/idX0KJIv72jXlc+E6VlZdR/3QFpRCdmWni2c/N4B2/uIi/bbXwtX8s4cQzm36pSnyngY9/YLxA4Xod3ysFMr/8/TZ+/EhyoITW3+Ww+H9qePcni7gtLEFygoAgIAjsKQKZHx91i6RmWtuN/uNPHXzcquHLd9XwLqU/dfDjRycBllc0n7bw4EGEy98AFu+r4xNTaCRPzsPl/bHH57ZHWkqWy9tB/TvAlwuWN9hd30b+Dd22gfwzC3jrekSAX0AO4VWU8WW/RBKCgCAgCAwPApk4BTNympk3zTXrzbxJ33f+m3P4y4+38Sdazd9XwbP35UA7D/o++4sUXK/X8eobZTxs2wF8cwVPf1PzKuDgXTod/f3kRyW8Wmi7Ti1aLSU9IPA97uRVv3pOn9Je3971uZLrmL0y3deE/126fRy9riddNP9fVPxxo8eP4qPrtd46r391uf71y2l3msP3fuTFY6VyrbOmlV9BYI8QyMQpkO5pI6mlpY/g83EVJ/xJIBdc7Izwkx8t4527JvEFKvt4Cwfr3or+jTLe+U4FLZ92FYseL/9C9euA1itV4PunuxxD0SRyHhcwj6/RjsX40IT0DNa6Hi0ZzSTbEwJNPFvaxsN6t9eax4VFz1ncVUSnRukm/uGn8HZoCfQ2ed9ccXeNfMc60NHfNJ5u1YBnzqCFDt5aXMexlrfTtcmXMkFgFxEY+J4C6aojqVH6a/c/i/999mllApXbPmnpbTzU8ZF5YV6vA8pZeC+opiMmoqHyu9hkTTsILONP14HSwWk8/akDV2NawS3grf/BLlC9S/jUvU9Ak7u+1xC+f0ATjXtx032CMF0Dx366id99XMBdzwTWnLgP+Pgni0GBpPpD4PpVdLCKdz63ytqX8SdMApjHw/9zHc/cN4Vj1Xl06I3TSfR8/BC3u9grqhl3PxlHb5T/5RsOnuaLhYOL+P73SzjxuQLUOOJ1PnNJCAK7j0AmToEip/GPmed1lDbrzbxJnyqvHUGqRpo4evzj7hLa/i5B3Wt4RNPrX3ImyzjIVnsRukccPKjJ6bhgEfi+OASNyOC/tn4nhw7gC48sId8GHjx4FRe0pDh6Xu71k25i/Y2jj5TX8Uk9zOG2L01R4IZwoeQEgT1GILPjI21H2khqaem1nIF+f7GBd/TO4ReV4P4CHf98PIUv6FWb3iXY7iVoBdR5cNgh6Cr53SUEDk4g/3EV/xB7n2gaT/OnxrrS74beTTz7HaD+afeHE3ZDG5EhCGgEBt4p0OOm76T4n0Jaeq1o5NfYnutHUiN0uiBET08beY+DHpxEp5SDvj9M23z3EVY666V7CcEuQbPiv5/84zp+h038rpTD//IqwsdKnFrSAyMQ6keX24n7ani3VcMzrB/V8aKxMg9ku2f63+uZPmjZcyqkp/uY823QCrmPQcMba6U3NnBXqYIvdH18umfpQigI9I3AeLwQjx3XyP8C+h4re9Yw8YV40rd71i8ieDQRGHinMJqwiFX7BoGDi/jxT/aNtqKoIDD0CIyHU5CJY+gHoigoCAgCw4FA5jeah8Ms0UIQEAQEAUGgHwRyqz/9Jwmy0w9y0kYQEAQEgRFEIOc4EnltBPt1pEy6dOkSjhw5MlI2iTGCwLAiIMdHw9ozopcgIAgIAnuAgDiFPQBdRAoCgoAgMKwIiFMY1p4RvQQBQUAQ2AMEMnkk9cUX4yOvPf54NPJaWvo9wEVECgKCgCAwmgh06igVtrHkrACVHDbmHKzw2GF0o3mQT71edz777LPYL9XzT1p6APR0VOhbLJedolEGFJ1ao2aUl50GF25NN5xyiFfRqbUdp10rhmQqHcoWbu2wzCI1tn7scqykUhhC4OLFi6G8ZAQBQWAwBBplb04t1hxzxsr8+KhbJDXT9Xajp4ejnHYNxWINbUo7DlqnJwGWVzROC4sUGI2XN4CZUh1eKBNTNMuX0fB4O8QnD+QXW0qWy9tBowwUJy2R19rbmGq4ejlOA1PVBdRjBUblMCUkKQgIAoLAriAwveLNWa1FmMGDM3EKZuQ0M29aadabeZO+7/z0HMqb22jTdqlUQaWUQy7nfivNFFw7dSyvlrFE3sL8TK+wrVcBk0WTQPJZIlDiTr5ZQU7lO6izvi3FeOVmJeh/tx2ApLFBdd54yeVKrrMPlXn89GAK1Xn0yvgmKj6fHCp1Go9ssaJ08PIhHhUEw9TgUan4Y1mPaWWT4mUb6y5GWlWA+JVQqZQQss3Ty8XKkx/SieFgs4HbQrbrvP41B4Nf7trn9x2Va8x1G1XG+pAw1TqYdVTu8/YY6PFCv6w/VFrzSZIVgKepXPt8Xry/gPjxxvpe62TqauZ9icY4oAFis53oQ+WsL7mtWr7PH8jEKRC/tJHU0tIznd3kZhUFvzPY4GCEnfoyVouTUOv7zS1MrnnesVHG6gzvwFXMeLz8Qcn4NM9Ugdpp8GM3Vh0kO+exjnnMWnyHS5QsJ2Akqe4INFGZ0UF18lhseX3brgHr5y27ww6ubhVRa3s7Ty7AOjaaqKhzV813HusL3sXMd6O0i92iID9x9DQZzwD+btLByiwXztPEo+rvPNu1LcyoicjCY2XF3cnyXbRe9VntyWNxqYzVDc/NNDewWl7CykoLTpvZRurQIggNOM4KpmPt4npnkZ7GCvVd9Qya6KC+sI75trtrD3E3seeVuo4w4eUqzcbLdAJ2vJ3mp08rVD9zgrj+IpqE8eazYDr5ZUkJyzjQk5LW1bc9STctwy4/E6egI6m9/oNjuHb916Bf+naLvNYrvTYh9KtB0Mc+/gUROIvC+jzaurzIJmvaQWALV9UxzzRWNA/b8Y+xS+jUaWXlrlbCDoQ6YR3za+52LErXRU7IOMl0Q6BZWcZkg1/83gqKJnLd5yEmbWzHxbOxjY3mVWwhcOK5QhWbtOsknnxBovu8E0OvFgo1nNYXr9YpxKPqhtohHsWANj87j+LqBppxPDQv89dmD411GvfED0BzYxXlOU+p/CLW5tdRUDZWUSCbtMJxduUnMKXxMOXbbCMaXp7LIbLwJj3IEeYKWJ9fU8e4Jut+89Hx0gMnrq/uZ94srr8UTcJ483hEdArJ88ZESB4tOoPxwasi6UTdXOqIfI9JJk6BIqfpL/HV6biIama9mY8YmKaAOwvr5JDELHr8Y+4S+L2Gln+cRBPSMibZysZOp2VH5ega+e0BgWYFy5Nr7j0kn9xzuu1JLOf4LtAjUBcJWxj47RISfCyphQOtnI37VrTKLnjy4uhtIjitv7qzEWZZNo258io2mk1srJahfQLtDBZoAaV3HY0pVPWuyLTXx2EaK3TPTu/WyaFoVeNsM8q3ltkxitc2P0HR6Pr4tLcD+WZz63gxiSz5kL6sny2kkaJu482mU0geX/BEuIcLkmwPUwY5m3yvNhOnEEgC0kZSS0vPZfWdpq2zXk01K8GKhVZkm1OY0Mc/xi7BKk+d24UdgpUuSY61gRRaEaDV1MYcAodspYoUds6vA/OzkZtqEUI9NqZpJVzFmeBQP0IaKlArZwt9fhbzsJSHGnsZgwfpvFmew3QaHiZfbY83pqdP17A1M4MtdhxKC5+pJXbDcfo0alpnQ6cQe30MQ44iE8dGxxl00tbtgY2QFirTuboFTE1E+7fP8RKVYCkxsPH7iw6PksZbvzrFjAOr7Qm6qR1bwjU08P8U6H8Iaf53kJbe0hVukdpqVVl1EbXGPMsbyRA9PQXkXQSFSWwVcsh55OWG4907oHNNupfQTryXoAYCNrFZyEFrU6y1o5NWrBxDT8l2QaCMRuihau+GGlupBn3osWpWUKjSOraAnO4kAAv1WbTofD9mbNAZd4mNDfVk25pJT/cpWmqMTNvoW4tYXAvzKddqMTa65+qBTBqn7hFPhEfDeLacc4yxR5HQxFJch77xRcecM3T/gMT4T83lPZ1LqLdb6qw/0MnbKaXehdtxy7NodJWce++FVJlubCBXqGBC3dfgxlnSqn/pUnWxClNYxkuYID4XwjHo56BBTH91G2/oVyfdL2y+KpexumqzPUa3zlWgm/zBnnbdJ63pvwSW53H3ifZjr+bA/1NolB0Y/zGh/6Go/5SM2tjoZg9hIdfCzl5TSeNtZyVnwn3gnULgNSUlCAwpAnTMYSwi6Z5Pi9T1V8dDqnvGaqkbzEtO9JglYzljzS5pvO0DYOTV2fugk8ZdRXl19riPALF/NxHI/EbzbiovsgQBQUAQEASyRSBH57XZshRugoAgIAgIAvsVATk+2q89N0Z6y/HRGHW2mLrnCMjx0Z53gSggCAgCgsDwICBOYXj6QjQRBAQBQWDPERCnsOddIAoIAoKAIDA8CGTyP4U0/2gm09PSDw9cookgIAgIAiOOwKB/gUsbSS0tvRl1jfL7M/Ka4zj0T0cvylt8hLZBe2T02g/8j+bRg0QsEgR2DIHMj4+6RVIzfWw3+pGJvEbBLNSrXdz386d9oZuJm+QFAUFAENgJBDJxCmbkNDNvKm7Wm3mTvu/8EEVea25sodb2Xr3ct0HSMBSxzI8a5UYVs8e5CDCLj4Rli1TmvWhPvxpaRwELRbOSyGv+W0IIF1u0s7hy3S26XkWCy8GPUaJw5tHrzP7wsNdRxBQ9i8pm00WPF/r1+9Xgw/UyaSIBIFzi2HEV057HWvGj3mm5/u+AEdaIjw0Tn398IhOnQOzTRlJLSx8xQb3B0BgEBtHwRF6j99dvokpv3PQGSsz4MiyQbDwCPGqURF5T8cv1m0sl8touRV6j0ZkQYc2Mj+BFbuOxVhyKXRF5P3sWEdbctzz78eNTvNo8E6cgkddocCRFXvNeV6sjvLXpnfaWQDDxM6DUGAhEo0ZJ5DUfIh0rhAp4lEGJvGZxFj5q0QRfeNoir6kWCRHW4trzFTyFlDXDfKaJtNdDhLWoYcklmTgFM3KamTdVMOvNvEmfKs+9s1459cwgGhEtm8hrE2EN1DvtdTjQcJXkekDAGjVKIq91R04ir3XHiFHwuYRH2GMkSIqwZmtPDoEcDMUKTxucKFWENTf2wtaMdzrB4o1w9W3pTJwCZ5w2klpaei6r7zSPRpUUES2zyGvuxbhc905gzQhvfRsyhg1p9ZUQNSoOkcRIWLyRHhsSec2NOmdE8OJQYdwjr9HhUVKEtRBYLMN2cm6QLlZHyawirFHfUUidRrrIeAP/TyFtJLW09AZcQVZtzVgYLQx35LXplTaulnTkL1sUp8A0SSUhYIlapVZfQYxgibxWRcEPMceiDBKsEnktaXCF60JzjOWa7RZhzdaewqJO5fz+KZbLliOtLCKs0Y6kCrqnoAIV+k8EhE205nbsYddhYtwtGtUw6Sq6RBAY+H8KSZGwRm1sdLNHIq9FxlffBUnjqm+me99w4J2C1dNIoSAwTAgkRcJKs4IaJpv61EUir/UJnK1Z0riy0e+TMnl19j7pqHFWU16dPc69L7bvNgKZ32jebQNEniAgCAgCgkB2CEjkteywFE6CgCAgCOx7BOT4aN934egbIMdHo9/HYuHwICDHR8PTF6KJICAICAJ7joA4hT3vAlFAEBAEBIHhQUCcwvD0hWgiCAgCgsCeI5DJ/xTSRlJLS7/nKIkCgoAgIAiMCwKD/n8ubSS1tPQ6Uhn/3Y+R19q1oh91zbel3BgU/rFoP/A/mscCJTFSEMgGgcyPj7pFUjOdbTd6/02C7I2DrdOTAMsrGqeFxQLC5Q1gRgfhMAWH8vR+GO+thcQnD4Teee44aJSB4iQJMD7tbfV+EVeHBqaqC9DvveOUPfPjjSQtCAgCgsAuI5CJUzAjp5l50yaz3syb9H3nhyjyWsiGXt6+GmogGY3AWEZe4+/f19G8dJSmUB2L0REqzyGnF0ehco+eynQ9RQap0OuWK2ga5SqSV1JEM9VJRsSwSkyUM5O37mC/3OUzNJHYtH5j8JuJUyCc0kZSS0sf6Qv1BsIgkpk/6Bnh8EReY0rRRXemCtROYzpcLLlUCIxT5DVjB0xRtFRgFgrs5L4Jk3aq7doWZrSzICz1btqPutWF3nMIG3O0a+41dCzvB0vEsJWVIG6A1qenOCfTWGnXgOoZNEFRxCgGgbuLDw0TzdMWm0DX+fbzlkxv/QpwotNtetKR8xuddCZOQSKv0YBIirzG3romu4RMrp6xirxGiPFFkI4CljbqVhK9x395su2+aln3Ukhu8HpyXR3qhzQRw0ybcjlwf6b45xexRo4uV8D6/Jo61tVyB/0N6T0osxFrn4lTMCOnmXkTM7PezJv0qfLa09PKIbW336nIa/QSdfcjuwSNxAC/4xh5jY/ruChgHNJUUbr0roLuiRXCk3NIbi387n9rP3AluqQN3lvLdbDlk2qcn6AwMX18kuwfVO8+1NlPTTJxCtzgtJHU0tJzWX2ndXQtmqt3JfKap6nsEvruMr8hrVzHLfKab7yRMKKiqShe5Tl1LNm5ugVMTSBYjlCAnQlMbVbdiGpe1LBNj97l7B7ZbM2UrA9LhKTb+iEmYlioXaoMHfEADSf+AY44dlb7idimdxyTMS0f+H8KaSOppaWP7Re1rd0/kdegzkXpXkJb7iXEdmovFWMYea1z1Ts+0uM9iAI23a6hVMghp6Cjp+im1UKnoIaaedfKnfQj9MRff/KLaLWheG7XarrU8mvpB1gihunIXxYO7pFY2KY86h4l3WhWHkFdL9ONDeQKFUz0cq9DRUSjS820n1jb9LYpN75l4/FCPHqiYQFYS32cNL4DY5gsH/iFeM0KchtzcFRcQteyTr2EBayhNXtexsYwdbbosucIDLxT2HMLRAFBoBsCSRGyzEPsbrykXhAYcQTGY6cw4p046uYNvFMYdYDEPkEgQwQyv9GcoW7CShAQBAQBQWCXEZDIa7sMuIgTBAQBQWCYEbgFnx9m9UQ3QUAQEAQEgd1EQI6PdhNtkSUICAKCwJAjIE5hyDtI1BMEBAFBYDcREKewm2iLLEFAEBAEhhwBcQpD3kHDrN6N107haP6o/33h0jBrK7oJAoJALwjc8tvzv8VXZr/i076QP4r3/BxLHH4Mb65/G7dS0aUXcPRhl+r4qxfxxBGPjpUHLQ/hsZ+/jG9/MdwuqAcUD3g8H3geF5fvAfAhXsg/qXRR9befw6lvvYQrXA+f5jie7zwBaqU+TI+Qfrreb+cXBAnif+oPeMizT1ccWnoTLx98y7dblyOkj19qJAJbeEXIbl4BQMk7qdAO1/zRw4GX+pjxQpZmePilPentUxuJGzg3/xBeupygp9FCsoKAILA/EPj/iQlLLPqPde0AAAAASUVORK5CYII=[/img] | |||
15.01.2018 09:40:55
| |||
15.01.2018 09:47:45
По моему расценки таблицы 46-04-003 более применимы в вашей ситуации. Во-первых потому, что в них единица измерения в м3, что позволяет в полной мере учесть весь объем демонтируемой стяжки (в ФЕРр 57-02-04 толщина лишь 150 мм учтена). Во-вторых - применяемые инструменты и механизмы - отбойные молотки (это то, что доктор прописал). В третьих - при применении расценок на устройство стяжки с коэффициентом на демонтаж следует учесть, что данные коэффициенты на демонтаж применимы только с сборным конструкциям (п.1, табл.2, гл.10, Пр. 81/пр от 09.02.2017) и незакрепленным, освобожденным от заделки в стены и другие конструкции, а также от сварки или иного крепления с другими конструктивными элементами (п.10.4, гл.10, Пр. 81/пр от 09.02.2017). Стяжка является конструкцией монолитной и она закреплена сама на себя.Трудовые процессы и применяемые механизмы при разборке монолитной конструкции коренным образом отличаются от трудовых процессов, приемов работ и применяемых механизмов при ее возведении. Кроме того, трудозатраты по разборке монолитной конструкции несоизмеримо выше трудозатрат по ее возведению и не могут учитываться | |||
15.01.2018 09:53:03
отбойным молотком разбирается 100 м2 покрытия, о какой толщине может идти речь? | |||
15.01.2018 10:01:45
Вот в измерителе "метр кубический" и идет речь о толщине. | |||||
15.01.2018 10:24:15
 | |||
15.01.2018 10:29:29
Но если переведем тонны мусора в кубические метры, а затем в сантиметры - то получится как раз толщина разобранной стяжки 150 мм (цифры не привожу. Проверьте меня!).
| |||||
15.01.2018 10:29:32
 | |||||
15.01.2018 10:37:59 Ирина Лисицина,возьмите ФЕР46-04-011-12 - выйдет не дорого и по технологии то, что надо
| |
15.01.2018 10:38:55 Алексей, меня объем более 1 м3 смущает в этой расценке, поэтому я склоняюсь больше к 11 сборнику, тем более и толщина стяжки всего 20 мм.
| ||||
